半路上车,Deep Learning 这块还在断断续续地慢慢学,但是由于现在测 TensorFlow 性能的需要,所以来学一下 AlexNet(额,听说 CNN 的计算量不少)。
AlexNet 是 2012 年 ImageNet 竞赛冠军获得者 Alex Krizhevsky 设计的,所以叫这个名字,这个也一直是入门 CNN 的经典模型。
组成部分分析
卷积层(Convolutional)
CNN 既然叫卷积神经网络,最重要的就是卷积了。
卷积这个操作是用于提取图像的某些特征,图像上的二维卷积其实与以前在信号系统中学过的一维卷积非常类似,公式大概是这个样子:
$$f[x,y]*g[x,y]=\sum_{n_1=-\infty}^\infty \sum_{n_2=-\infty}^\infty f[n_1, n_2] \cdot g[x-n_1, y-n_2]$$
用卷积核 g 对图像 f 作卷积就是将 g 沿着反对角线翻转,然后跟 f 上的对应位相乘,对相乘之后的所有位求和,所得的值作为卷积结果图的一个像素。
CNN 中由于卷积核全是随机生成的,反对角线翻转这一步就不需要了。
对应的几个术语:
kernel_size 表示卷积核的大小;stride 表示一次卷积之后,卷积核平移几个像素;pad 是对原图的边缘进行像素扩充。
池化/降采样层(Pooling)
选定一个区域进行降采样就是留下一个值,主要用于减少数据量。
降采样的方法通常有取区域中的最大值留下,或者对区域中的像素求均值留下(滑动平均?)等等。
激活函数层
额,就是应用一个激活函数…
常用的有 sigmoid、tanh、ReLU 等等函数,要看需要把值控制在什么区间范围内,然后反向求导的时候是不是好算……(话说选什么激活函数完全是经验+玄学吧?数学原理在哪里?)
标准化/归一化层(Normalization)
有的实现里面能看到这个,有的没有,一般就是用个公式对数据进行归一化一遍。
全连接层(Fully Connected)
接上一个深度神经网络,没啥好说的。
遗忘层(Dropout)
以一定概率随机(纯随机哦…)扔掉一些数据,不加很容易造成过拟合。
据说是为了模拟人脑的过程(???)
反正在我这里看来怎么看怎么玄学,是不是换个随机数生成器都可能有不同的效果?
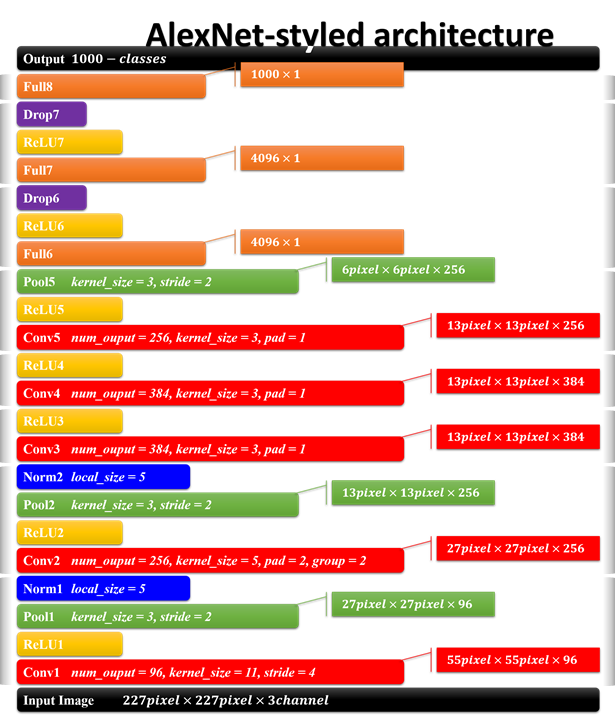
Alexnet 结构详解
第一阶段
输入的是一些 227*227 大小的图像,RGB 三个通道,这是初始数据。
第一个卷积层用的是 96 个大小为 11*11 的卷积核,stride=4 表示每次卷积完了之后移动 4 格,所以一张 227*227 的图经过一次卷积之后就会变成 $\frac{227-11}{4}+1=55$ 边长的图,3 个通道做完之后数值相加。96 个卷积核所以得到了 55*55*96 这样的数据。
中间过一遍激活函数,ReLU。
第一个降采样层用了 3*3 的采样核,stride 为 2,则每张图通过之后得到了 $\frac{55-3}{2}+1=27$ 边长的数据,一共为 27*27*96 个像素点。
第二阶段
输入从 27*27*96 开始。
第二个卷积层用的是 256 个大小为 5*5 的卷积核,stride 这里是 1,pad=2 是扩充边缘,即对前面 27*27 的图像的上下左右四个方向各扩充 2 个像素变成 31*31 的图像,这是为了防止卷积操作使得图像大小缩小得过快。所以由于 pad 参数的存在,经过卷积之后图像的大小是 $\frac{27+2*2-5}{1}+1=27$ 没有发生改变。group=2 指定的是把前面 96 个通道分成 2 个子集,数据的累加在各自的子集内完成。输出是 27*27*256。
过一遍激活函数。
然后第二个降采样层与第一次一样,得到了 $\frac{27-3}{2}+1=13$ 边长的数据,一共 13*13*256。
第三阶段
输入从 13*13*256 开始。
第三个卷积层用了 384 个大小为 3*3 的卷积核,pad=1,则得到了 $\frac{13+2*1-3}{1}+1=13$ 边长的图,一共 13*13*384。
过一遍激活函数。
第四阶段
输入从 13*13*384 开始。
第四个卷积层用了 384 个大小为 3*3 的卷积核,pad=1,则得到了$\frac{13+2*1-3}{1}+1=13$ 边长的图,一共 13*13*384。
过一遍激活函数。
第五阶段
输入从 13*13*384 开始。
第五个卷积层用了 256 个大小为 3*3 的卷积核,pad=1,则得到了$\frac{13+2*1-3}{1}+1=13$ 边长的图,一共 13*13*256。
过一遍激活函数。
第五个降采样层用了 3*3 的采样核,stride=2,则得到了 $\frac{13-3}{2}+1=6$ 边长的图,一共 6*6*256。
第六阶段
输入从 6*6*256 开始。
连接了 4096 个隐层节点。
开始时这一部分我不是很明白,以为 6*6*256 的数据怎么就变成 4096 个了,后来看了代码的实现才知道是把前面的 $6*6*256=9216$ 个像素作为输入层的 9216 个节点,跟接下来的 4096 个隐层节点全连接起来。所以这里的权值 W 是个 9216*4096 的矩阵,偏置 B 是长度为 4096 的向量。
过一遍激活函数。
再接一个 Dropout,随机把这 4096 个数据中的某些丢掉置为 0。
第七阶段
输入从 4096*1 开始。
继续连接 4096 个隐层节点。
权值 W 是个 4096*4096 的矩阵,偏置 B 是长度为 4096 的向量。
过一遍激活函数。
继续 Dropout。
第八阶段
输入从 4096*1 开始。
连接 1000 个输出层节点。
权值 W 是个 4096*1000 的矩阵,偏置 B 是长度为 1000 的向量。
输出的 1000 个数据对应的就是分在 1000 个类别的概率了。
To be continued.