接上篇:
写着写着越写越多了,所以想想还是分成多篇来了,要不一页内容有点多。
Control Flow in TF
从 Executor 的运行实现里面往下继续的时候遇到了点问题,代码里面有个叫 Frame 的概念,但是注释里面很多东西都写的不清不楚的,不知道在干吗,于是在网上找了点关于 TF 的整个控制流方面的资料:
- Request for documentation: Loop implementation - GitHub
- Implementation of Control Flow in TensorFlow
核心的问题是从 TensorFlow 的循环控制里面引出来的,这块内容具体涉及到的也其实就是 TensorFlow 中的数据流模型的实现了,这里的数据流模型原型是基于 Jack Dennis 和 Arvind 等人所提出的数据流机。
TensorFlow 中,每一个 Op 都在一个 Execution Frame(前面看代码见到的结构)中运行,由以下五种控制流原语来负责 Execution Frame 的创建和维护。例如每个 while 循环在跑的时候都会先创建一个 Execution Frame,然后循环里面的所有 Op 都会在这个 Frame 里面完成运行。Frame 也可以嵌套,比如说嵌套的循环就会有嵌套的 Frame。不同 Frame 中的 Op 只要相互之间没有依赖的都可以并行运行。
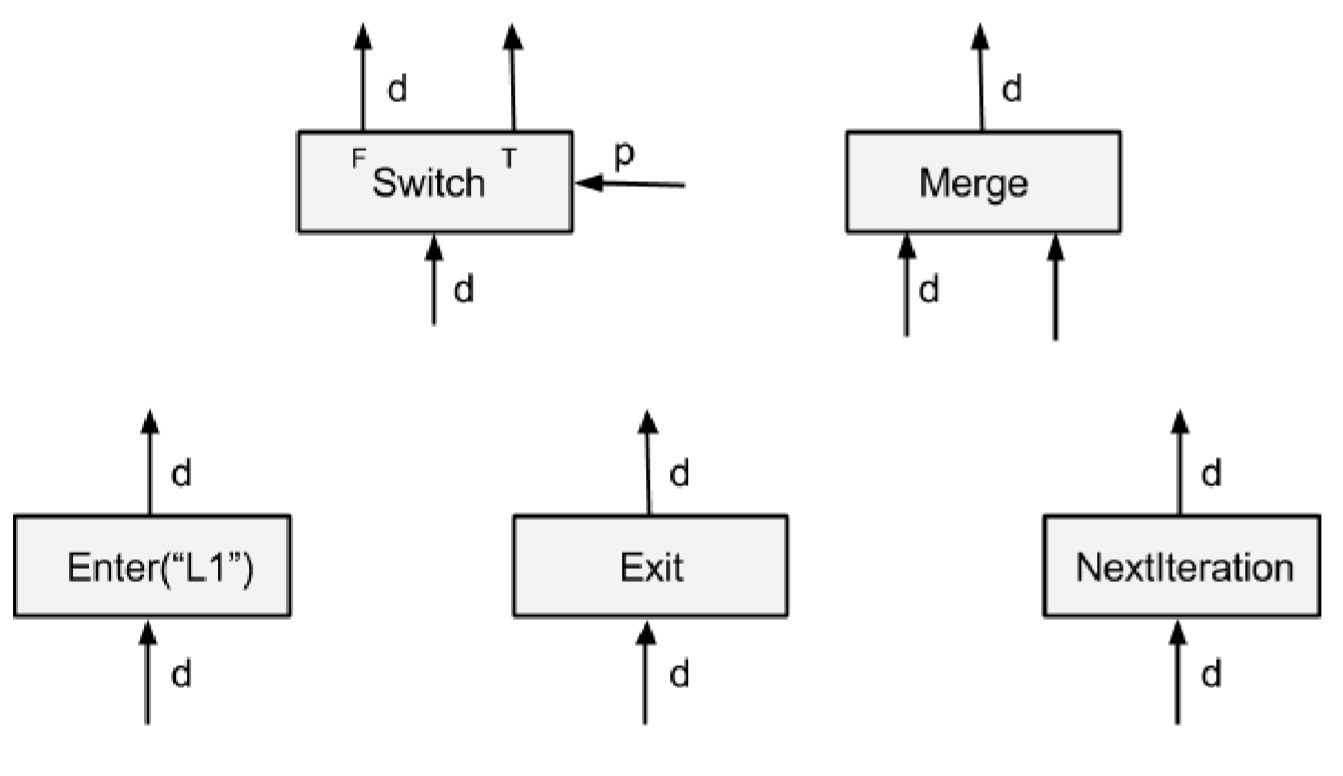
- Switch:根据控制 p,把输入 d 传到某个输出里。只要 d 和 p 都可用时就可以执行
- Merge:把某个输入传到输出里。只要有任意一个输入就能执行,如果有多个输入都可用,这里并不会指明最终会输出哪一个输入
- Enter(“name”):把输入传到某个 Frame 里。这个 Op 用于把一个 Tensor 传到某个子 Frame 里去。一个 Frame 也可以有多个 Enter Op,Frame 在它的第一个 Enter Op 执行的时候完成实例化
- Exit:从某个子 Frame 中把数据传出来(传给它的父 Frame)。一个 Frame 也可以有多个 Exit Op
- NextIteration:把输入传到当前 Frame 的下一次迭代中。例如 while 循环的每一次迭代执行的 Op 是一样的,TF 运行时会记录下 Frame 的迭代次数。一个 Frame 中也可能会有多个 NextIteration Op。当第 N 次迭代中的第一个 NextIteration Op 执行的时候就开始了第 N+1 次迭代,第 N 次迭代每提交一个 NextIteration Op,第 N+1 次迭代就会有一个 Tensor 输入可用,然后激活后续执行的 Op
用上述的这几个原语就可以完成一些复杂操作了,例如:
1 | tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y)) |
可以这样实现:
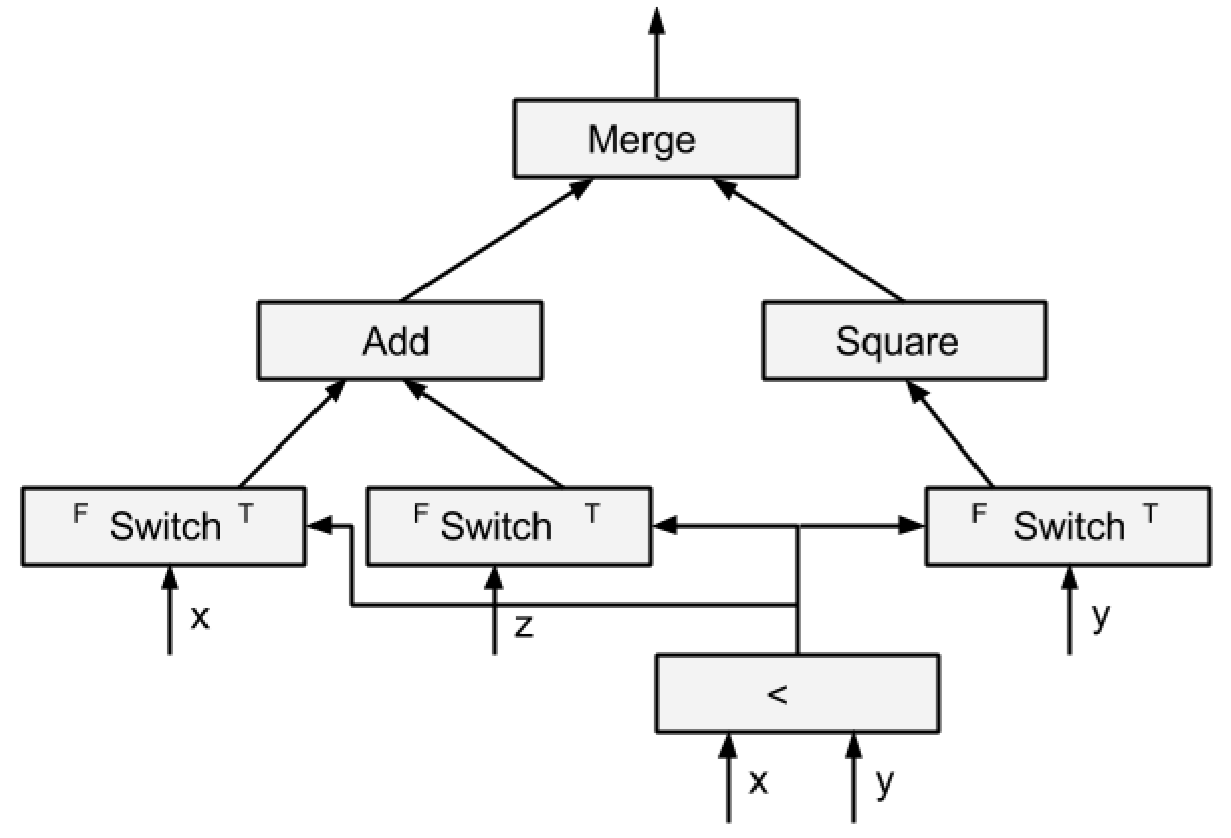
然后对于一个 while 循环:
1 | tf.while_loop(lambda i: i < 10, lambda i: tf.add(i, 1), [0]) |
实现出来是这样的:
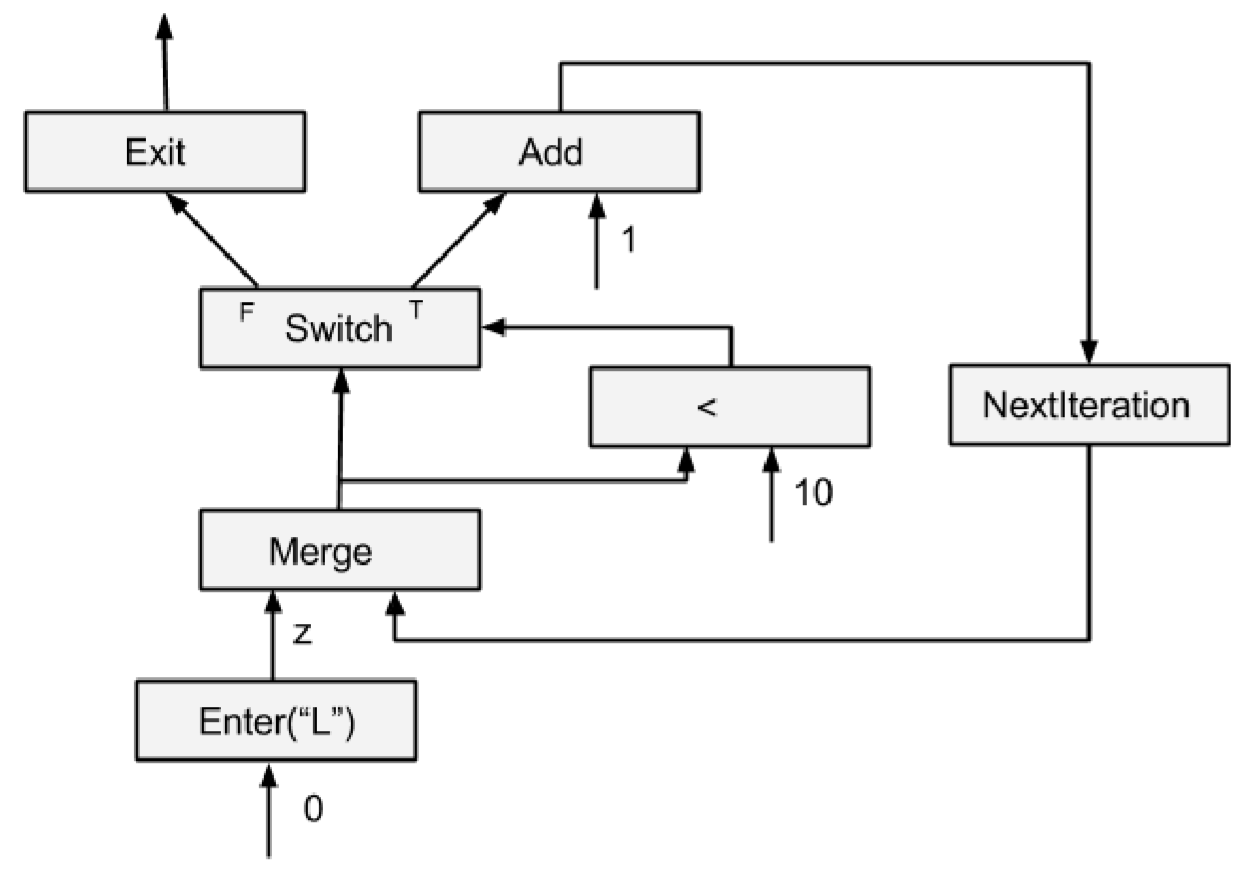
上面这个例子里面的循环非常简单,当循环更复杂一点,例如变量有多个时,就会有多个 Enter、多个 NextIteration 和 多个 Exit Op。这样每一层迭代中的不同部分就能够充分发挥并行性。
Executor 中运行产生的每个 Tensor 都可以用一个三元组来表示(value, is_dead, tag),value 显然是实际的数据,is_dead 用于标识当前 Tensor 是不是在一个选择语句的 untaken branch 上(感觉怎么翻译都难受,还是原文好),tag 这个标记是唯一的,其中包含了 Executor 上下文信息、Tensor 的生产者等等,在 send/recv 的过程中 tag 也是通信 key 的一部分。
分布式环境下有可能出现条件选择语句在 Device A 上,某个分支的具体执行在 Device B 上的情况。运行时中遇到 source node 都是无条件执行的,例如 recv Op 也是一种 source node,所以实际实现的时候会做 is_dead 标记的广播。
Distributed While Loop
再来看一下分布式环境下的循环是怎么实现的。
一种 naively 的实现是这样的:
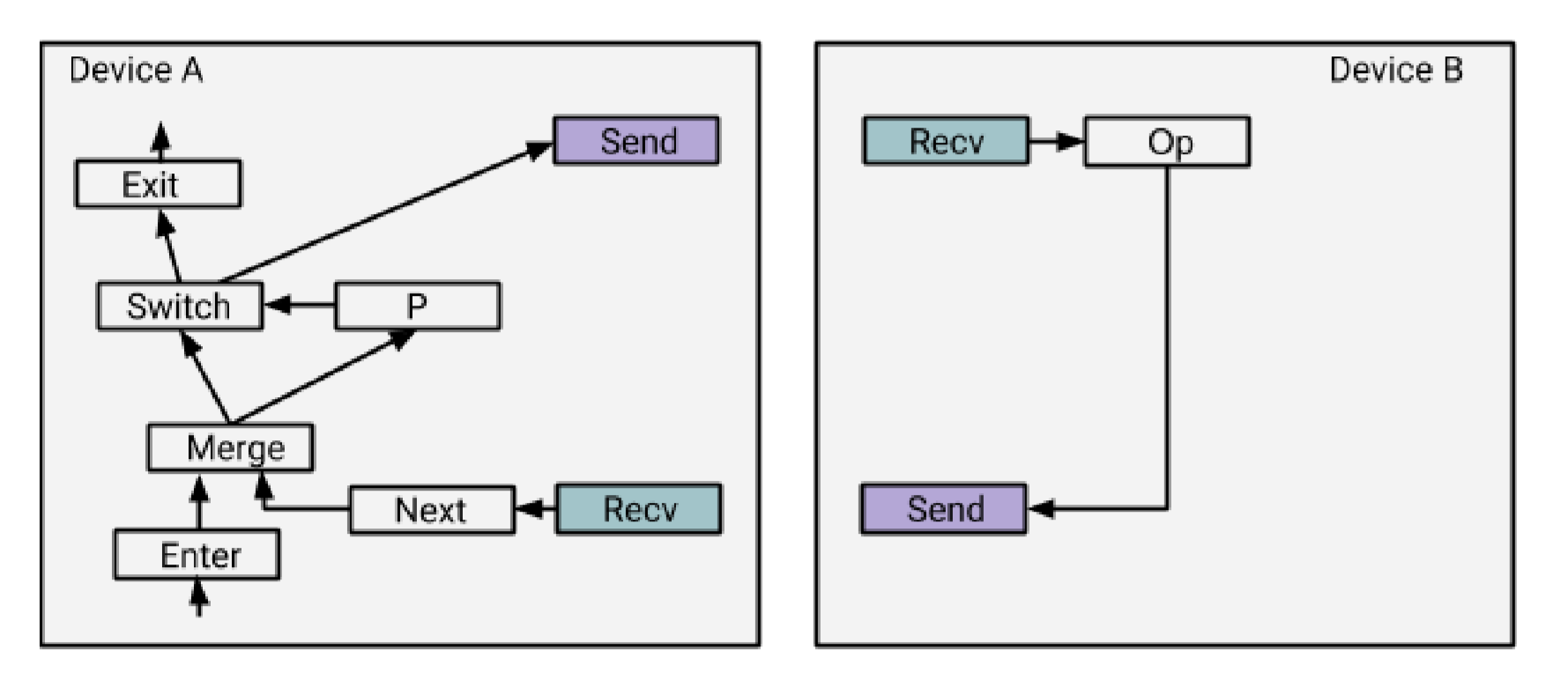
这里比较尴尬的的是,循环的控制体在 Device A 上,循环体却是在 Device B 上(话说实际会有这种划分方式吗?想一下 GPU 的运行是不是就是这样的呢?控制 batch 和 epoch 的部分在 CPU 上,然后中间实际的图的运算在 GPU 上?)。
按照前面原本的实现方式,Device B 并不知道自己所跑的子图是一个循环的一部分,因此按照正常情况来处理,它所负责的每个 Op 都只执行一次就结束了,那如果要让这个循环一直跑下去,可能就要在每次 Device A 调用 send 之后,Device B 再创建一个新的 Executor Frame,果然是 naive 啊。
TensorFlow 的解决方案是:
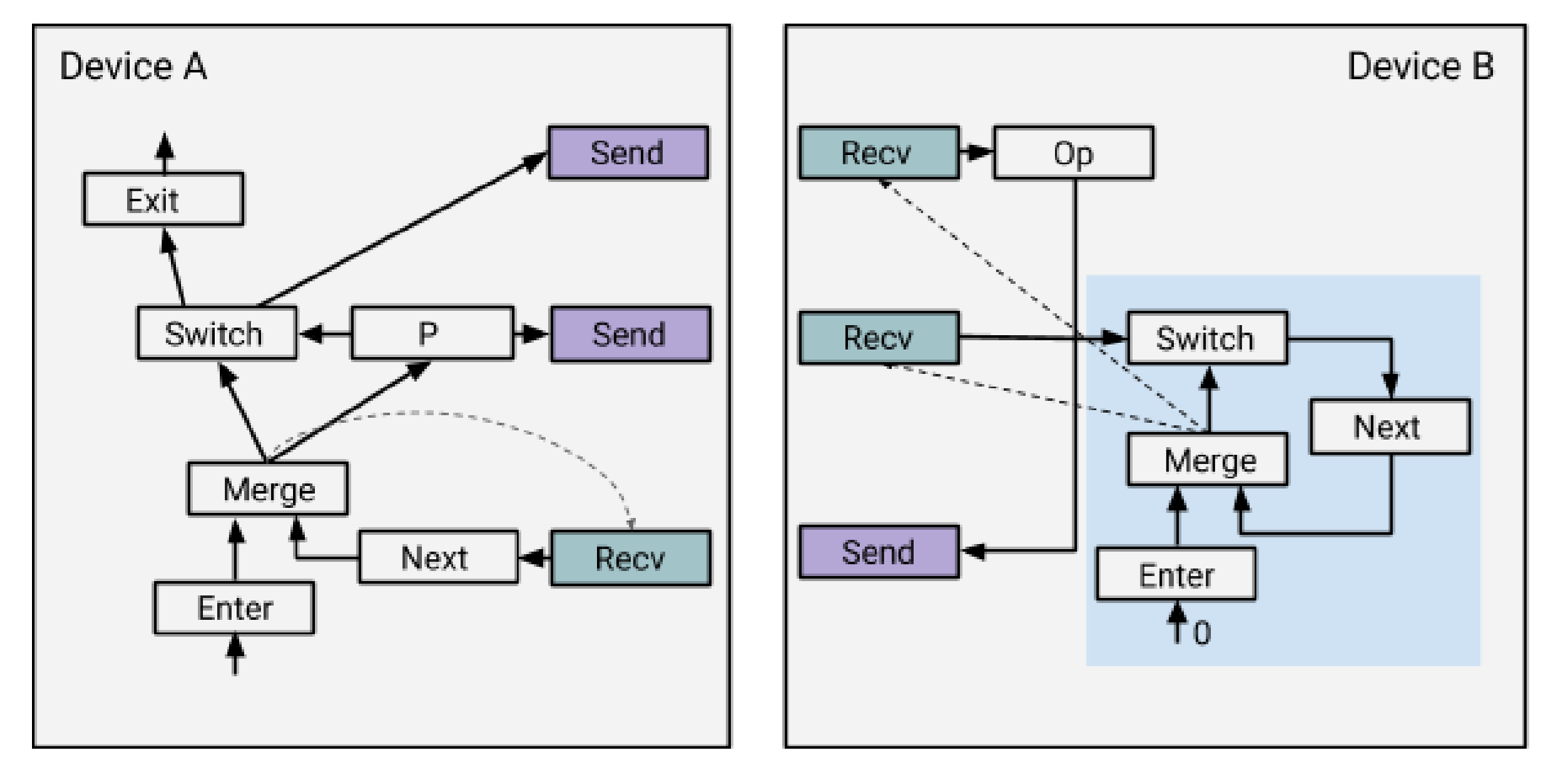
在 Device B 上加上一个控制循环的状态机,把 Device A 中的 switch 和 next 也加到 B 上去。使用这种方式实现的循环在更多设备参与的更复杂循环中能够发挥出更好的并行性。例如 Device B 只要接收到了 P 就能开始下一层迭代或者退出了,而不用等到 Device A 跑完循环的其他部分,多个不同的设备也可以在同一时刻跑着一个循环的不同迭代层的内容。接收一个 P 的开销可以被高度的并行性隐藏掉。
嵌套循环的情况类似,也是继续构造一个状态机,把外层循环的 switch 输入到内层循环状态机的 Enter 里去即可。
Automatic differentiation
首先需要理解 BP 算法里面的梯度计算规则,参考资料在这里:
基本原理就是链式求导法则,这里有个前向求导和反向求导的区别,例如对于一个这样的计算过程:
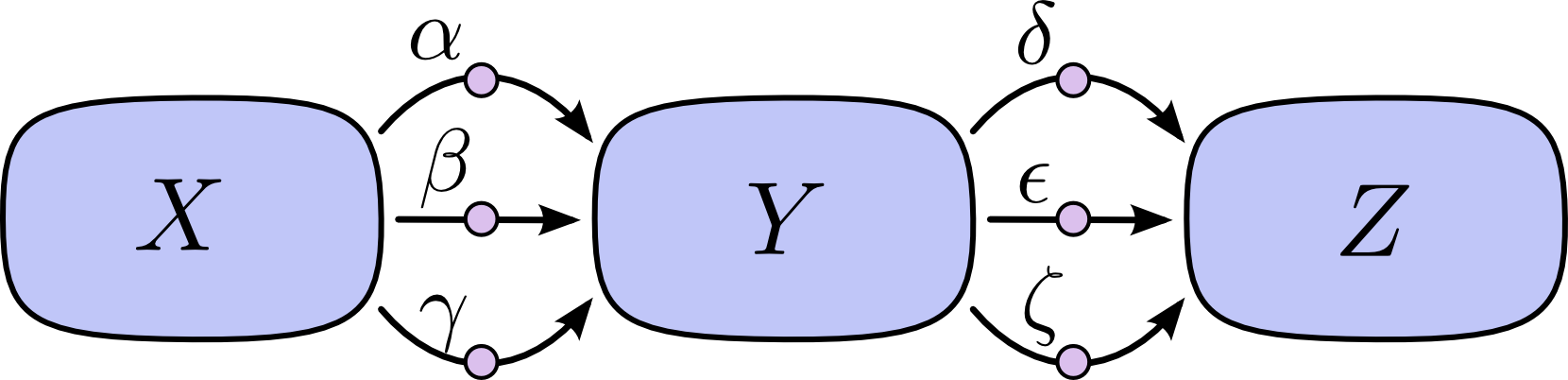
前向求导是从第一层开始,逐层计算梯度 $\frac{\partial}{\partial X}$ 到最后一层:
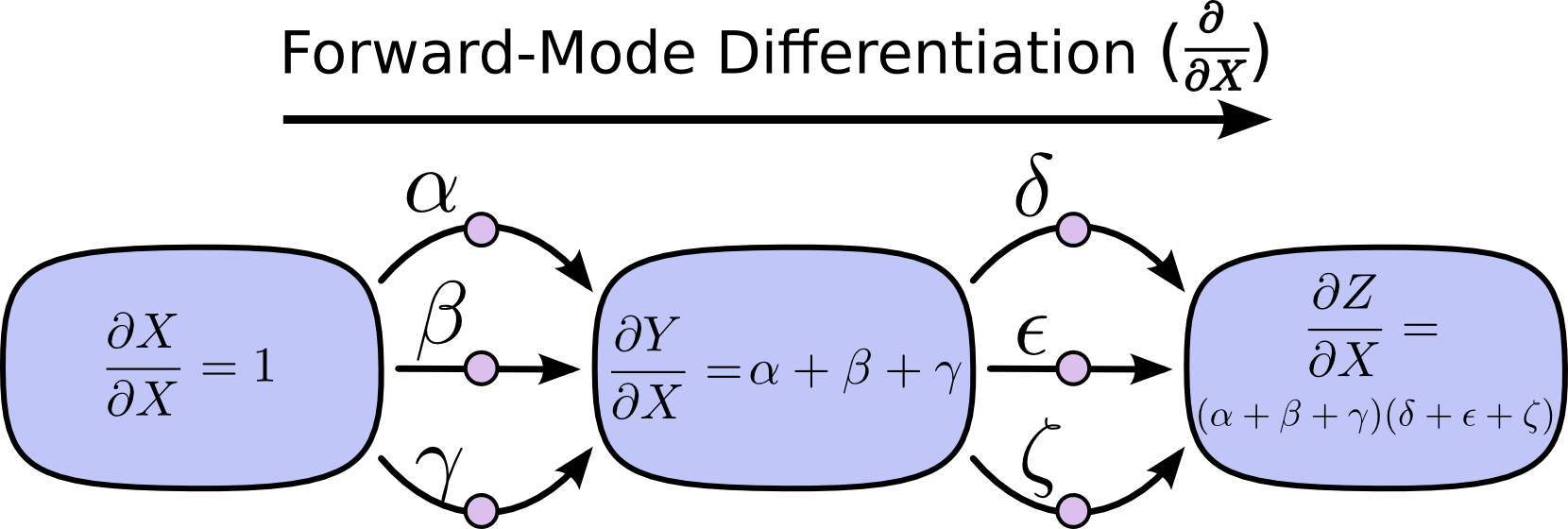
反向求导是从最后一层开始,逐层计算梯度 $\frac{\partial Z}{\partial}$ 到第一层:

前向求导关注的是输入是怎么影响到每一层的,反向求导则是关注于每一层是怎么影响到最终的输出结果的。
对于一个多输入单输出的计算网络,如果想要得到每个输入和输出之间的关系,用前向求导需要对每一个输入都做一次,而用反向求导则只需要做一次就可以得到输出和每个输入之间的关系。
对于单输入多输出的计算网络,则应该用前向求导才能一次获得一个输入对多个输出的关系。
神经网络中每一层的参数都算是一种输入,可以说是输入数量远大于输出数量的情况,因此用反向求导更加合适。
举个栗子:
假定有一个网络,输入数据是 $X_{in}$(形状是 N x D),结果一共有 C 种分类,则对应的 Label 一共有 N 个,处理之后每一个都是一个 1 x C 的向量,每个向量中都只有唯一一个位置是 1,代表了这个样本属于哪个类,其他 C-1 个位置都是 0,设这个对应的结果是 $Y_{label}$ (形状是 N x C)。
网络有多个层,每层有参数($W_i$ 和 $b_i$):
这个过程写成公式大概是:
$$
\begin{align}
Y_0 &= f_0(W_0, b_0, X_{in})\
Y_1 &= f_1(W_1, b_1, Y_0)\
Y_2 &= f_2(W_2, b_2, Y_1)\
&…\
Y_n &= f_n(W_n, b_n, Y_{n-1})\
Y_{out} &= Softmax(Y_n)\
\end{align}
$$
BP 算法的训练过程则是根据网络计算得到的 $Y_{out}$ 和实际的真实结果 $Y_{label}$ 来计算误差,并且沿着网络反向传播来调整前面公式中提到的所有 $W_i$ 和 $b_i$,使误差达到最小。
强调一下,深度学习里面 BP 的本质目标是让误差达到最小,所以要用误差对中间出现过的所有影响因素求偏导。
最后一层的误差和梯度:
$$
\begin{align}
Error &= Loss(Y_{out}, Y_{label})\
\Delta{W_n} &= \frac{\partial Error}{\partial W_n} = \frac{\partial Error}{\partial Y_n}\frac{\partial Y_n}{\partial W_n}\
\Delta{b_n} &= \frac{\partial Error}{\partial b_n} = \frac{\partial Error}{\partial Y_n}\frac{\partial Y_n}{\partial b_n}
\end{align}
$$
看一下上面两个等式右边的部分,$Y_n$ 对 $W_n$ 和 $b_n$ 的导数只与第 n 层的计算有关(全连接、卷积或者其他什么,每一种层都直接有自己固定的梯度计算公式)。
$Error$ 对 $Y_n$ 的导数则是要看最后的损失函数(最常见的如 Softmax 和交叉熵)怎么定义,也有直接固定的梯度计算公式
倒数第二层以后:
$$
\begin{align}
\Delta{W_{n-1}} &= \frac{\partial Error}{\partial W_{n-1}} = \frac{\partial Error}{\partial Y_{n-1}}\color{red}{\frac{\partial Y_{n-1}}{\partial W_{n-1}}}=\frac{\partial Error}{\partial Y_n}\frac{\partial Y_n}{\partial Y_{n-1}}\frac{\partial Y_{n-1}}{\partial W_{n-1}}\
\Delta{b_{n-1}} &= \frac{\partial Error}{\partial b_{n-1}} = \frac{\partial Error}{\partial Y_{n-1}}\color{red}{\frac{\partial Y_{n-1}}{\partial b_{n-1}}}=\frac{\partial Error}{\partial Y_n}\frac{\partial Y_n}{\partial Y_{n-1}}\frac{\partial Y_{n-1}}{\partial b_{n-1}}\
\Delta{W_{n-2}} &= \frac{\partial Error}{\partial W_{n-2}} = \frac{\partial Error}{\partial Y_{n-2}}\color{red}{\frac{\partial Y_{n-2}}{\partial W_{n-2}}}=\frac{\partial Error}{\partial Y_{n-1}}\frac{\partial Y_{n-1}}{\partial Y_{n-2}}\frac{\partial Y_{n-2}}{\partial W_{n-2}}=\frac{\partial Error}{\partial Y_n}\frac{\partial Y_n}{\partial Y_{n-1}}\frac{\partial Y_{n-1}}{\partial Y_{n-2}}\frac{\partial Y_{n-2}}{\partial W_{n-2}}\
\Delta{b_{n-2}} &= \frac{\partial Error}{\partial b_{n-2}} = \frac{\partial Error}{\partial Y_{n-2}}\color{red}{\frac{\partial Y_{n-2}}{\partial b_{n-2}}}=\frac{\partial Error}{\partial Y_{n-1}}\frac{\partial Y_{n-1}}{\partial Y_{n-2}}\frac{\partial Y_{n-2}}{\partial b_{n-2}}=\frac{\partial Error}{\partial Y_n}\frac{\partial Y_n}{\partial Y_{n-1}}\frac{\partial Y_{n-1}}{\partial Y_{n-2}}\frac{\partial Y_{n-2}}{\partial b_{n-2}}\
&…\
\Delta{W_0} &= \frac{\partial Error}{\partial W_0} = \frac{\partial Error}{\partial Y_0}\color{red}{\frac{\partial Y_0}{\partial W_0}}\
\Delta{b_0} &= \frac{\partial Error}{\partial b_0} = \frac{\partial Error}{\partial Y_0}\color{red}{\frac{\partial Y_0}{\partial b_0}}
\end{align}
$$
公式里面标红的部分都只与该层的计算内容相关,直接有梯度公式。
那么另外的那部分呢……$Error$ 对 $Y_i$ 的求导其实可以一路链式求下去:
$$
\begin{align}
\frac{\partial Error}{\partial Y_{n-1}} &= \frac{\partial Error}{\partial Y_n}\frac{\partial Y_n}{\partial Y_{n-1}}\
\frac{\partial Error}{\partial Y_{n-2}} &= \frac{\partial Error}{\partial Y_{n-1}}\frac{\partial Y_{n-1}}{\partial Y_{n-2}}=\frac{\partial Error}{\partial Y_n}\frac{\partial Y_n}{\partial Y_{n-1}}\frac{\partial Y_{n-1}}{\partial Y_{n-2}}\
&…\
\frac{\partial Error}{\partial Y_i}&=\frac{\partial Error}{\partial Y_{i+1}}\frac{\partial Y_{i+1}}{\partial Y_i}=\frac{\partial Error}{\partial Y_{i+2}}\frac{\partial Y_{i+2}}{\partial Y_{i+1}}\frac{\partial Y_{i+1}}{\partial Y_i}=…
\end{align}
$$
这中间 $Y_{i+1}$ 对 $Y_i$ 的求导即每一层的输出对输入求导,也是只与每层的计算内容有关。
这就是整个神经网络的完整训练过程了。
话说,链式求导法则本身很简单,关键这里面的每个变量都坑爹的是个矩阵啊。。。矩阵对矩阵求导的具体计算要涉及到矩阵微分了,这个恕我数学不好,没学过。。。溜了。。。
这里有一个关于怎么求矩阵和矩阵的梯度的介绍:
TensorFlow 的做法是每一个 Op 在建图的时候就同时包含了它的梯度计算公式(即上面公式中的 $\frac{\partial Y_i}{\partial Y_{i-1}}$、$\frac{\partial Y_i}{\partial W_i}$、$\frac{\partial Y_i}{\partial b_i}$),构成前向计算图的时候会自动建立反向部分的计算图,前向计算出来的输入输出会保留下来,留到后向计算的时候用完了才删除。
对前面描述的5个控制流原语来说,反向的梯度部分很大程度就是把整个图翻一下,Enter 和 Exit 互换、输出和输入互换、Switch 和 Merge 互换等等,当然很多细节上还要再修正一下。
看到这个地方我感觉有点明白了为什么要设 Frame 这个概念了。
有 Enter 和 Exit 这两个控制流原语在,再加上数据流图单向依赖的这个特性,图的结构是具有结合律的,一个大 Frame 就能很方便地拆成多个子 Frame。
反向求梯度的这个过程是一样的,以 Frame 为单位反向串起来就好。
PropagateOutputs()
接上篇,后面回来看看一个 node 处理完了之后是怎么做后续的新 node 的,这里就出现了前文提到的 Frame 的概念。
tensorflow::(anonymous namespace)::ExecutorState::PropagateOutputs()根据当前处理的 node 的类型分成了 4 种情况:
普通计算 node:
调用
tensorflow::(anonymous namespace)::ExecutorState::FrameState::ActivateNodes()来激活当前 node 的后继 node,主要内容是检查后继 node 的依赖是否满足,是则加入 ready 队列;调用
tensorflow::(anonymous namespace)::ExecutorState::FrameState::DecrementOutstandingOpsLocked()来递减当前 frame 的当前次迭代的 outstanding_ops,减到 0 的时候就表示当前次迭代已经完成了。Enter node:
tensorflow::(anonymous namespace)::ExecutorState::void ExecutorState::FindOrCreateChildFrame(),进入一个子 Frame,如果是第一次调用 Enter,则创建一个新的 Frame;判断是否作为循环变量,否则作为一般 node 处理,调用 ActivateNodes() 激活后继 node;
DecrementOutstandingOps()。
Exit node:
退出当前 Frame,用 ActivateNodes() 激活父 Frame 中的后继节点;
DecrementOutstandingOps()。
Next_iter node:
判断目标迭代次数是否达到,如果是就保存状态退出;
继续迭代则调用
tensorflow::(anonymous namespace)::ExecutorState::FrameState::IncrementIteration进入下一个迭代,如果是第一次调用,会对下一次迭代做初始化;DecrementOutstandingOpsLocked()。
到这里为止,当前 node 的计算过程才算完全结束,之后再对 node 所属的 Frame 判断一下是否结束即可。
Optimizer in TF
引用一下这个知乎问题:
回到 TensorFlow 的 Python 代码层面,自动求导的部分是靠各种各样的 Optimizer 串起来的,构图的时候只需要写完前向的数据流图部分,然后在最后加上一个 Optimizer(例如 GradientDescentOptimizer、AdamOptimizer 什么的),然后调用它的 minimize() 方法就会自动完成反向部分的数据流图构建。
tensorflow/python/training/optimizer.py 中定义了所有 Optimizer 的基类,从介绍中可以看到,整个反向通路的构建过程其实是分成三个部分的:
- 计算每一个部分的梯度,
compute_gradients() - 根据需要对梯度进行处理
- 把梯度更新到参数上,
apply_gradients()
minimize()的完整定义:
1 | def minimize(self, loss, global_step=None, var_list=None, |
它就是一次性把上面这些都做了,函数体中只有很短的几行,串起计算流图,逐层计算梯度,往最小化 loss 的方向更新 var_list 中的每一个参数。
compute_gradients
那么再来看一下compute_gradients()做了什么事情:
- 如果没有给定 var_list,则这里会去自动找到计算图中所有的 trainable_variables 放到 var_list 里面去,这些就是整个网络中的参数
- 往图中插入一个 gradients 的 Op,所以很明显反向求导的这个串图的过程就是在这里完成的了!!
- 这个方法的返回结果是一个
(gradient, variable)的 list
接下来就看看 gradients,先来做一个简单的测试:
1 | In [2]: a = tf.Variable(1) |
g 中的两个部分分别是对 a 和 b 进行求导的结果。后面创建一个 tf.Session() 跑一下得到的 g 是 [3, 1]。
gradients 的实际定义在 tensorflow/python/ops/gradients_impl.py中。把整个求导过程抽象成一个 $ys = f(xs)$ 的函数,xs 就是 var_list 里面输入的变量(在这个过程中其实这里存的是每个变量对应过来在计算图中的 op)。
根据原本计算图中所有的 op 创建一个顺序的 list,这个顺序在图上来说其实也是拓扑序,反向遍历这个 list,对每个需要求导并且能够求导的 op(即已经定义好了对应的梯度函数的 op)调用其梯度函数,然后沿着原本图的方向反向串起另一部分的计算图即可(输入输出互换,原本的数据 Tensor 换成梯度 Tensor)。
这里有个叫 gate_gradients 的输入参数,用于控制梯度计算过程的并行性。
GATE_GRAPH 很好理解,即整个图中间的梯度计算(后向过程)和梯度更新是单独分开的,计算过程严格按照前向、后向、更新的步骤来,等到所有的参数都完成梯度计算之后,再统一发起更新。
GATE_NONE 和 GATE_OP 的差别在于梯度更新会不会影响到后续的其他计算。例如某个 op 有 n 个输入 $x_0, x_1, …, x_{n-1}$ ,梯度的计算和更新需要对所有这 n 个输入求导,在 GATE_NONE 模式下,$x_0$ 的梯度计算完了之后,对 $x_0$ 的更新就马上开始了,那么在算其他输入(例如 $x_{n-1}$)的梯度时,有可能此时 $x_0$ 的值已经变了(数学上来说这就 bug 了吧?),因此按注释中说的可能会出现“不可复现”的结果,因为这个过程不可预料,是先更新完还是梯度先计算完,可能跑两次的结果都不一定一样。
GATE_OP 即产生一些控制依赖,确定某个变量不再会被用到之后才进行更新,保证正确性的同时最大化并行性。
事实上 TensorFlow 中所有的 op 的并行性是由其数据流计算模型来保证的,实现上来看,GATE_GRAPH 是在所有梯度计算 op 后面加上一个 control_flow_ops,GATE_OP 类似。
apply_gradients
接下来的这个部分是根据前面求好的梯度,增加一个更新前面涉及到的所有参数的操作,Optimizer 基类的这个方法预留了_create_slots(),_prepare(),_apply_dense(), _apply_sparse()四个接口出来。
后面新构建的 Optimizer 只需要重写或者扩展 Optimizer 类的某几个函数即可,所以在 TF 给出的几个默认的 Optimizer 定义都不是很长。
apply_gradients()核心的部分就是对每个 variable 本身应用 assign,如果有设了 global_step 的话,顺便再加个 1。
在看这部分的时候我还有个问题,
global_step是怎么保证在多个 worker 同时写的情况下不发生写冲突,在代码中并没有发现任何处理多线程上锁或者队列等等的操作。
后续: