把去年 7 月的那篇 TF 删掉了，重新开一篇。

2016.07.10

初次接触 TensorFlow，当时主要是面临 RDMA 竞赛，题目的目标是 TensorFlow 的 RDMA 优化。

分析之后发现这玩意有点大，不确定是否能够来得及整个剖析一遍，只好关注于 TensorFlow 里面的通信模块（gRPC）的 RDMA 化了。

只是对 TensorFlow 的分布式版做了一些很小的测试，更多的还不太了解。

2016.11.07

写了个：

未来可能要花很长时间在这玩意上了。

初步确定之后有个大方向是围绕 TensorFlow 展开。

2016 学年末

TensorFlow 这艘大船搭上了实验室的很多人，主要是实验室看上了 TensorFlow 的数据流框架：

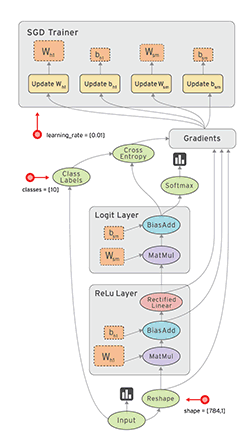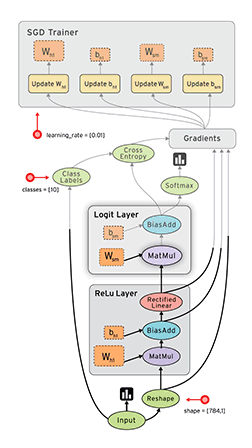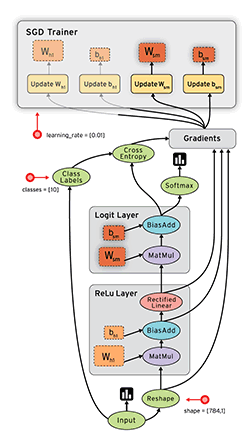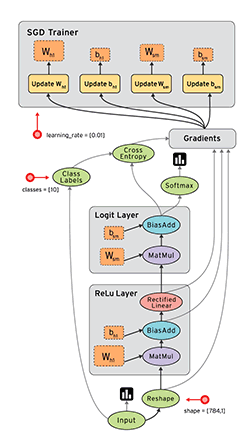
深度学习是一方面，另外的想法是是否可以以 TensorFlow 为基础，用数据流来支持其他类型的计算，如并行科学计算等等。

按之前 RDMA 优化下来的感觉，TensorFlow 的并行性能还是受 gRPC 限制，我的任务方向是着手考虑是否能够把整个 gRPC 都拿掉，用例如 MPI 等等的办法来替代其中的通信交互。

期间也见过一些其他人改出来的 “MPI 版 TensorFlow”，都是在外面跑一个 MPI 的调度框架，然后里面跑单节点版的来避开 gRPC 的影响。

Example

其他的介绍啥的暂时不写了，直接记一些干货吧。

以下是一个来自 github 的例子。

该例做的是一个简单的线性回归，即给出一些已知点来拟合一条直线。在 TensorFlow 里面可以直接视作一个训练的过程。

import tensorflow as tf
import numpy
import matplotlib.pyplot as plt
rng = numpy.random

# 设定后面需要的一些参数
learning_rate = 0.01
training_epochs = 2000
display_step = 50

# 给出训练数据，就是两个坐标数组了
train_X = numpy.asarray([3.3, 4.4, 5.5, 6.71, 6.93, 4.168, 9.779, 6.182, 7.59, 2.167, 7.042, 10.791, 5.313, 7.997, 5.654, 9.27, 3.1])
train_Y = numpy.asarray([1.7, 2.76, 2.09, 3.19, 1.694, 1.573, 3.366, 2.596, 2.53, 1.221, 2.827, 3.465, 1.65, 2.904, 2.42, 2.94, 1.3])
# 坐标点的个数
n_samples = train_X.shape[0]

# tf Graph 的输入部分，这里创建了两个占位符
X = tf.placeholder("float")
Y = tf.placeholder("float")

# 建立模型

# 模型的权重和偏值
W = tf.Variable(rng.randn(), name="weight")
b = tf.Variable(rng.randn(), name="bias")

# 激活函数是一个乘加的线性模型，A = X * W + b
activation = tf.add(tf.mul(X, W), b)

# 最小化方差
# 这里调用了 TensorFlow 里面内置的优化函数，每次都算出方差 cost，再调用内置的梯度下降算法在给定的学习率的条件下优化方差到最小
# ... 说白了整个线性回归就 optimizer 这里是有用的，然而直接用的 TF 的内置函数来完成了
cost = tf.reduce_sum(tf.pow(activation-Y, 2))/(2*n_samples) #L2 loss
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost) #Gradient descent

# 变量的初始化器
init = tf.initialize_all_variables()

# 启动 TensorFlow 的流图计算
with tf.Session() as sess:
    # 首先初始化所有变量
    sess.run(init)

    # 训练 training_epochs 次
    for epoch in range(training_epochs):
    	# 把输入的两个序列 train_X 和 train_Y 中对应位置的数打包成 (x, y) 的结构
        for (x, y) in zip(train_X, train_Y):
            # 运行 optimizer 就是训练过程了，每次训练都使得 W 和 b 朝着使方差 cost 最小的方向更近一步
            sess.run(optimizer, feed_dict={X: x, Y: y})

        # 过某特定步输出一次 log
        if epoch % display_step == 0:
            print("Epoch:", '%04d' % (epoch+1), "cost=", \
                "{:.9f}".format(sess.run(cost, feed_dict={X: train_X, Y:train_Y})), \
                "W=", sess.run(W), "b=", sess.run(b))

    # 上面循环完之后整个线性回归的过程就结束了
    print("Optimization Finished!")
    print("cost=", sess.run(cost, feed_dict={X: train_X, Y: train_Y}), \
          "W=", sess.run(W), "b=", sess.run(b))

    # 把结果显示出来，这里用了 matplotlib 这个库
    plt.plot(train_X, train_Y, 'ro', label='Original data')
    plt.plot(train_X, sess.run(W) * train_X + sess.run(b), label='Fitted line')
    plt.legend()
    plt.show()

这个例子得益于优化算法完全由 TensorFlow 里面自己来实现了，所以写起来非常简单。

TensorFlow 在深度学习中的使用方法就这么简单，类似上面这个例子：

建立数据流图
在 Session 中启动数据流图，把数据喂进去

然后数据跑完一遍，留下的参数就离最优解更近一步。

之后的重点就是看看 Session.run() 以及内置的这些 tf.train.xxx 函数在代码里面是怎么实现的了。

TensorFlow Unpacking

2018年新年启动

开始 TensorFlow 比较完整的源码分析记录：