继续有想法就多写点硬一些的内容。
关于计算机系统中的运算部件硬件实现,我脑子里面能想到的最近一次接触这些的时间可能还要追溯到在学校里面学数电那会了,而且大多数东西都忘得差不多了,刚好重新理一理并且顺便看一下浮点运算部件到底是怎么做的。
目前我们工作中并不会涉及到太深入到芯片设计方面的内容,因此本篇也只是对基础做一些整理,能帮助在脑子里面形成一个对不同运算部件的大体概念就不错了,充其量用这些在 MC 里面搞搞红石电路啥的。
篇尾还想找找 Nv 的硬件 spec 稍微对比分析下看看。
这里推荐一个各种不同运算算法在电路上的模拟网站:
通过上面的一些例子的模拟可以帮助更好地理解整个过程是怎么实现的。
整数运算 - ALU
先看看基础的二进制整数运算部分。
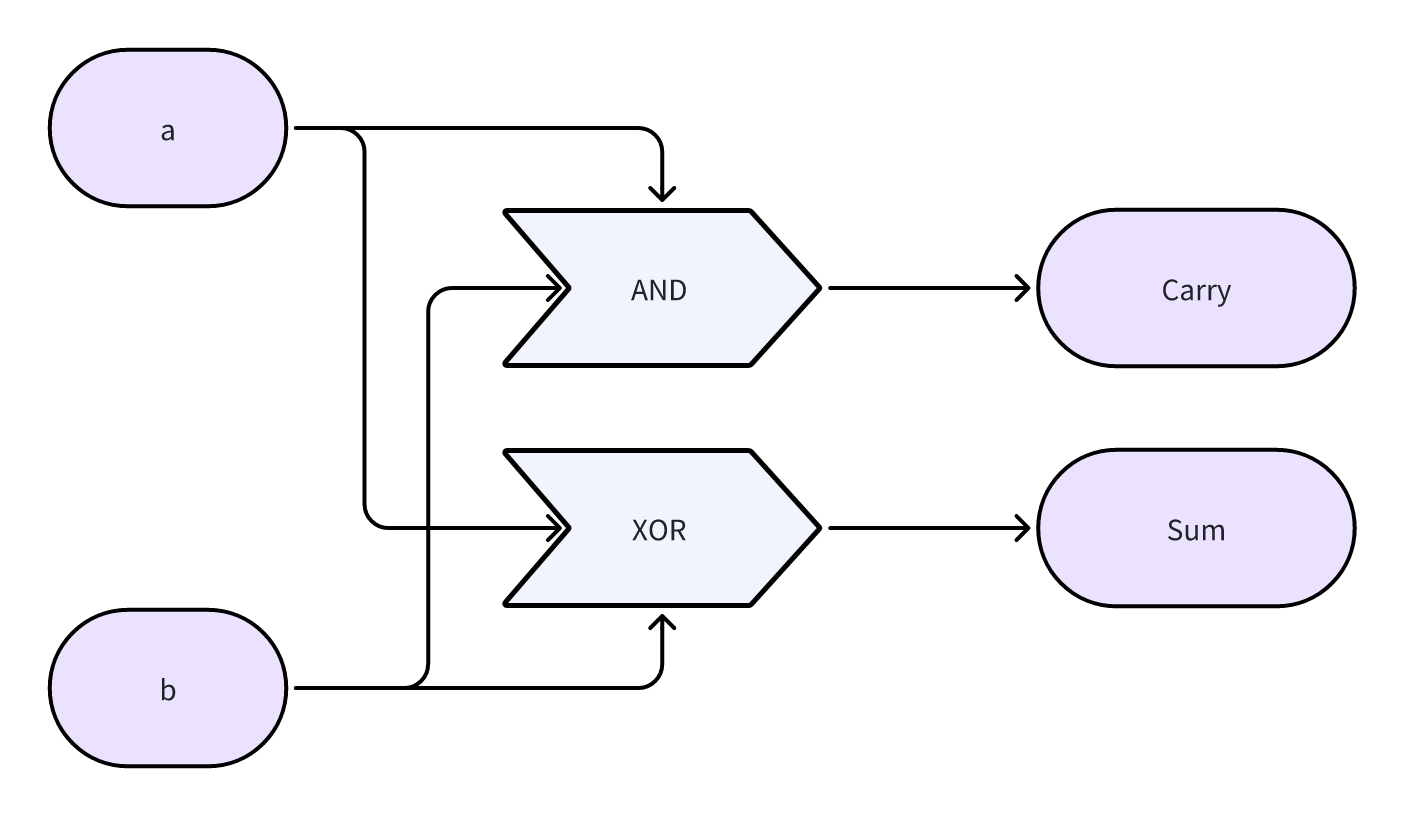
半加器(HA)
可以算是所有运算中最基础的部件了,功能是将两个输入 bit 加在一起,输出结果(Sum)和进位(Carry)。
| a | b | Sum | Carry |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
可以很容注意到,Sum 和 Carry 的输出可以用两个门电路来得到:
- Sum = a XOR b
- Carry = a AND b
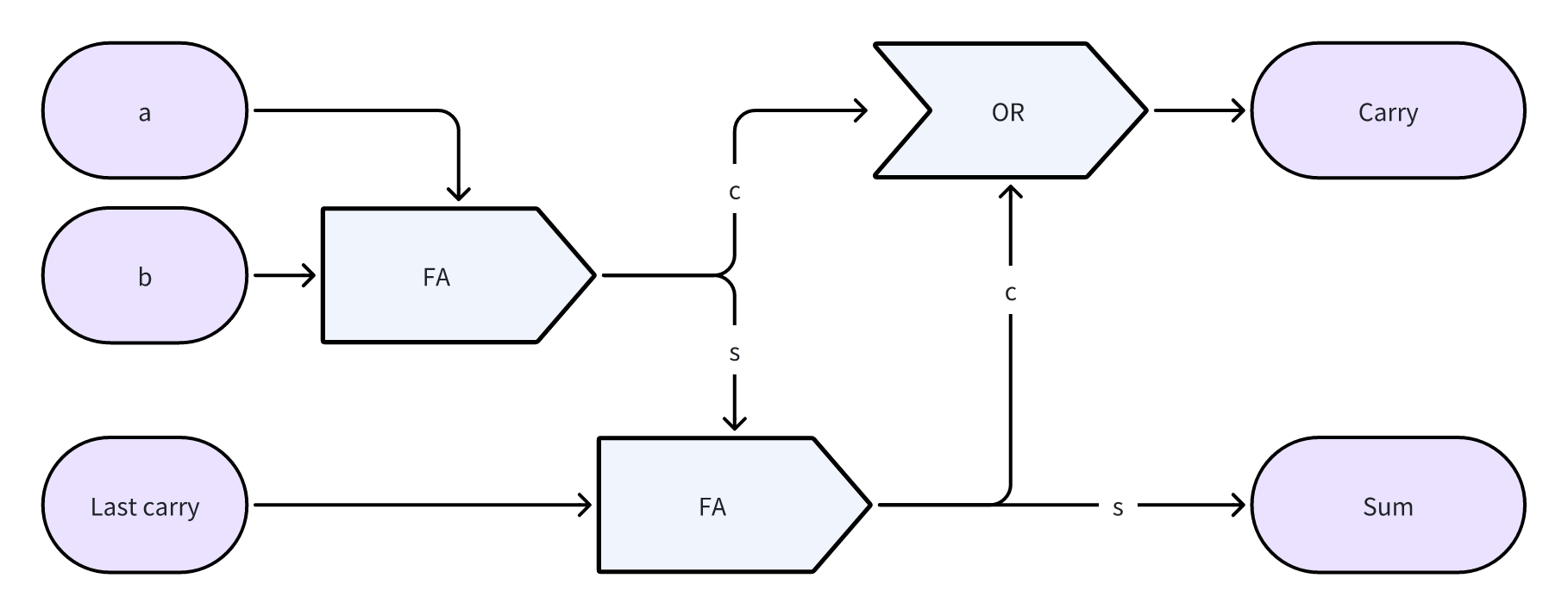
全加器(FA)
多位二进制加法运算中考虑到每一位都有可能向前进位,因此对 3 个 bit 位进行加法操作的运算才是更常用到的,用两个 HA 串联在一起可以共同实现:
| a | b | Last Carry | Sum | Carry |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
门电路实现:
- s0 = a XOR b
- c0 = a AND b
- s1 = s0 XOR c
- c1 = s0 AND c
- Sum = s1
- Carry = c0 OR c1
多位加法器
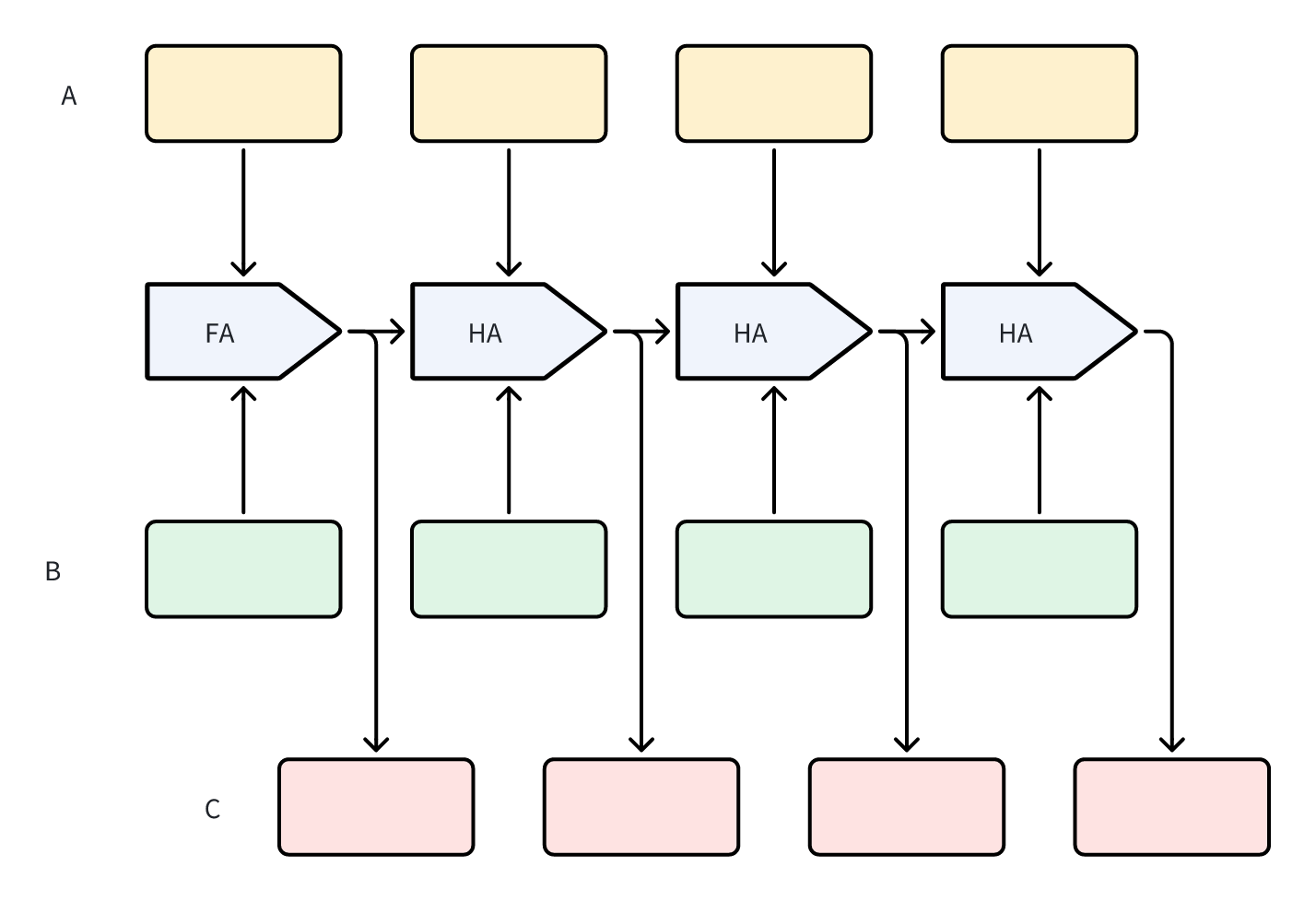
逻辑上,通过任意数量的 FA 串联就能实现任意长度 bit 位数的加法运算,实际中需要结合硬件的物理情况进行考虑设计电路,例如 cmos 工艺、电路上的信号延迟等等。
如果直接用以上的基础实现进行位数规模扩展,整个芯片的效率会很低,因此在此基础上还有例如超前进位加法器、并行前缀进位加法器等等更加高效的实现。
乘法器
单 bit 位的乘法器只是一个 AND 的逻辑:
| a | b | Prod |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
考虑多 bit 位的情况,运算过程其实与 10 进制下的乘法竖式计算是一致的,a、b 中的每一位对应相乘时需要附带一个偏移(其实也就是个加权一维卷积过程):
| a1 | a0 | |
|---|---|---|
| b1 | b0 | |
| a1b0 | a0b0 | |
| a1b1 | a0b1 | |
| a1b1 | a1b0 + a0b1 | a0b0 |
$$\begin{aligned}
A &= a_1 * 2^1 + a_0 * 2^0 \\
B &= b_1 * 2^1 + b_0 * 2^0 \\
A*B &= a_1b_1 * 2^2 + (a_1b_0 + a_0b_1) * 2^1 + a_0b_0 * 2^0
\end{aligned}$$
因此我们可以得到一个通过不断移位和累加就能够完成的乘法器设计思路:
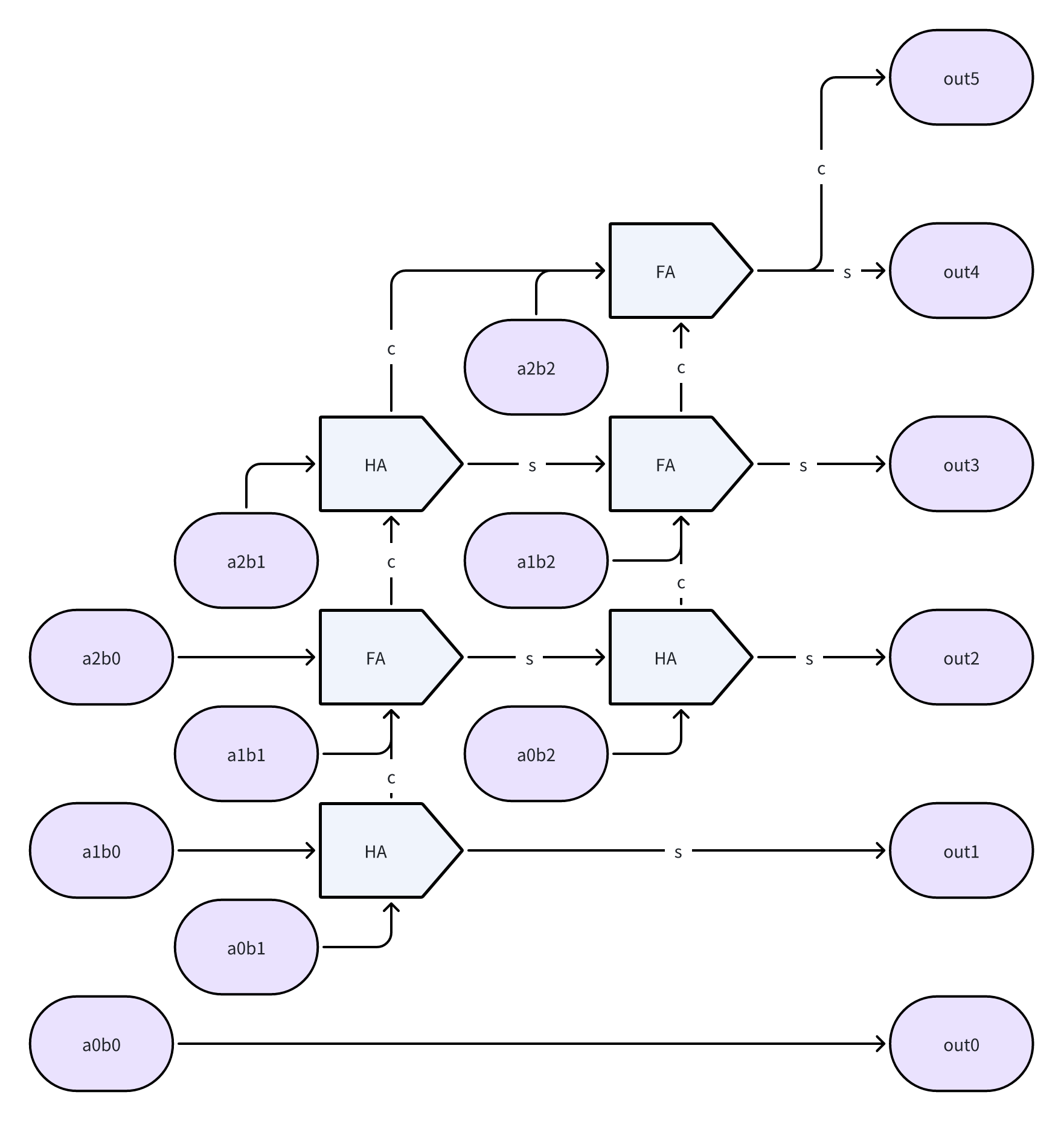
与多位加法器类似,如果直接按照最简单的硬件逻辑来实现电路的话的效率会很低,也非常不利于进行更多 bit 位的扩展,因此也衍生出了 Booth、Wallace树、Dadda、SRT 等等优化算法。
除法器
考虑 10 进制下对每一位进行试除和累积余数的竖式计算方法,我们可以得到一个类似的除法器设计思路:
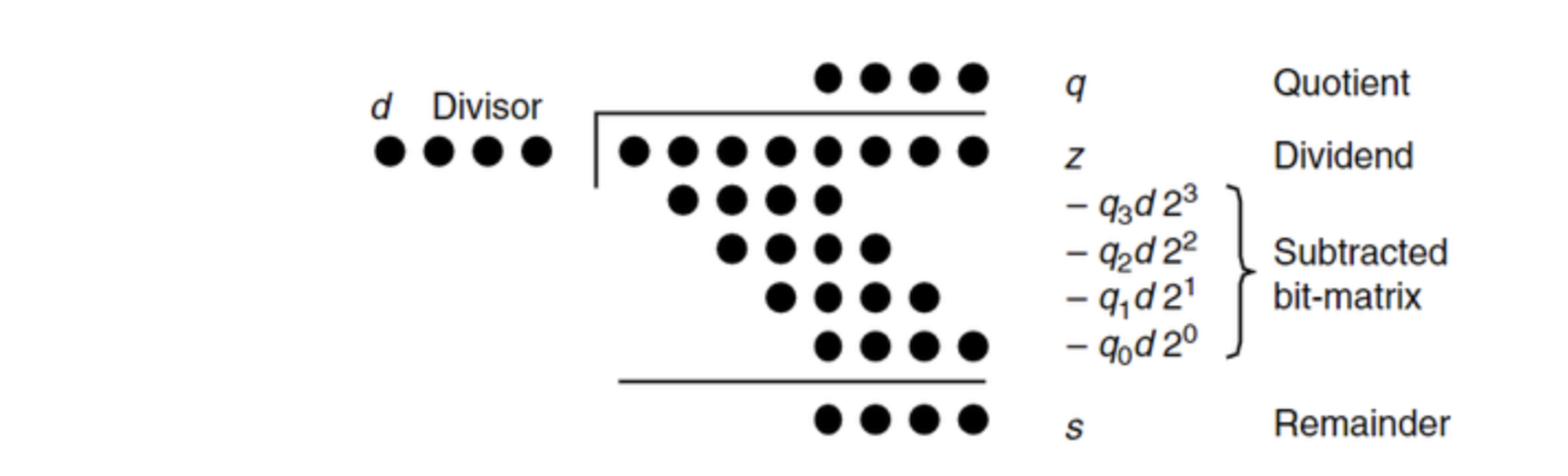
恢复余数除法
这里来推一遍 10 / 3,在 8 位二进制下除法的过程:
| Source | A = 10 = (00001010)2 D = 3 = (00000011)2 |
|
|---|---|---|
| Init | D 初始时左移 A 的 bits 变成 00110000 | |
| Step 1 | 左移 A -> 00010100,A = A - D < 0 | 则该位结果为 0,A 保留余数 00010100 + 0 |
| Step 2 | 左移 A -> 00101000,A = A - D < 0 | 则该位结果为 0,A 保留余数 00101000 + 0 |
| Step 3 | 左移 A -> 01010000,A = A - D = 00100000 >= 0 | 则该位结果为 1,A 保留余数 00100000 + 1 -> 00100001 |
| Step 4 | 左移 A -> 01000010,A = A - D =00010010 >= 0 | 则该位结果为 1,A 保留余数 00010010 + 1 -> 00010011 |
最终得到的结果为:
R = A[4:7] = (0001)2 = 1
Q = A[0:3] = (0011)2 = 3
由于初始计算时 D 本身已经偏移了 A 的 bits 数,因此 A - D 的正负性不回受后面补上的除完结果影响,因此这里为了简化一个寄存器,结果的 Q 直接更新在 A 中了。最终计算截断前 4 位为余数,后4位为结果。如果要继续往后面推算小数部分,则 Q 应该独立更新。
为什么这个算法要叫做恢复余数算法呢?
注意到上述计算中判断 A = A - D < 0 的这一步,事实上这里需要先发生减法运算,对结果进行 test 判断小于 0 之后,再把 D 加回去,恢复出 A,因而被称为恢复余数算法。
不恢复余数除法
那么 A - D < 0 的时候能不能不用恢复到 A 再往下走?答案是可以的,相比于不恢复余数法整体上算法复杂一些,但是在硬件实现上更有优势。
这里每产生一个商的比特位只需要一次加或减操作,核心是在减法操作后不需要进行余数恢复,这样就使得执行的速度更快了。
继续以 10 / 3,在 8 位带符号二进制下除法的过程举例:
| Source | A = 10 = (000001010)2 D = 3 = (000000011)2 -D = -3 = (100001101)2 |
|
|---|---|---|
| Init | D 初始时左移 A 的 bits 变成 000110000 -D 左移变成 111010000 |
|
| Step 1 | 左移 A -> 000010100,A 是正数,A = A - D = 111100100 < 0 | 则该位结果为 0,A 保留余数 111100100 + 0 |
| Step 2 | 左移 A -> 111001000,A 是负数,A = A + D = 111111000 < 0 | 则该位结果为 0,A 保留余数 111111000 + 0 |
| Step 3 | 左移 A -> 111110000,A 是负数,A = A + D = 000100000 >=0 | 则该位结果为 1,A 保留余数 000100000+1-> 000100001 |
| Step 4 | 左移 A -> 001000010,A 是正数,A = A - D = 000010010 >=0 | 则该位结果为1,A保留余数 000010010+1 -> 000010011 |
最终得到的结果为:
R = A[4:7] = (0001)2 = 1
Q = A[0:3] = (0011)2 = 3
再往后还有 SRT、高基除法等等更多性能更好或者更适合电路实现的变种和改进算法,这里不再展开。
浮点数运算 - FPU
浮点数的表示
首先看一下将小数部分直接进行二进制转换的表示法:
$$
(00001100.00001100)_2 = 2^3 + 2^2 + 2^{-5} + 2^{-6} = 12.046875
$$
用 2 的幂次直接来指代小数部分可以提供的范围和精度都非常有限,尤其截断之后产生的误差会相当大,因而一般通常大家讲到定点数时一般都用来指代整数了,比较少有场景直接这么用。
对于以下 x、y 两个数,数值范围上差别很大,但如果写成科学计数法的方式来表示,则写法上非常相似:
$$\begin{aligned}
x &= (00000000.00001001)_2=(1.001) * 2^{-6} \\
y &= (10010000.00000000)_2=(1.001) * 2^7
\end{aligned}$$
并且我们可以发现,用这种方式可以同时兼顾较大的数值范围和较高的精度。
在 IEEE 754 标准中,将浮点数的表示为:1 个符号位 + e 个指数位 + f 个尾数位的形式。
以 float32 为例,规定为 1/8/23 的格式。指数位有 8 位,是一个 0~255 的整数,用 Exp 移位之后的结果来表示,其中 0 和 255 这两个值被用来作为特殊标记,尾数有 23 位:
| E + Bias | Frac | |
|---|---|---|
| 表示 0 | 0 | 0 |
| 表示低于精度下限的非正规数 $0.f * 2^E$ |
0 | 非 0 |
| Inf | 255 | 0 |
| NaN | 255 | 非 0 |
| 常规浮点数 $1.f * 2^E$ |
[1, 254] E -> [-126, 127] |
任意数 |
因此 float32 能够表示的绝对值的最小值为($2 ^ {-126} + 0$),最大值小于($2^{128}$)。
| Sign | Exp | Frac | Max Value | Min Value Normal | Min Value Subnormal | |
|---|---|---|---|---|---|---|
| float16 | 1 | 5 | 10 | $2^{15} * \sum^{0}_{i=-10}2^i = 65504$ | $2^{-14} = 6.10 * 10^{−5}$ | $2^{-14} * 2^{-10} = 5.96 * 10^{−8}$ |
| float32 | 1 | 8 | 23 | $< 2 ^ {128} \approx 3.4 * 10^{38}$ | $2^{-127} \approx 1.18 * 10^{−38}$ | $2^{-127} * 2^{-23} \approx 1.4 * 10^{−45}$ |
| float64 | 1 | 11 | 52 | $< 2 ^ {1024} \approx 1.80 * 10^{308}$ | $2^{-1023} \approx 2.23 * 10^{−308}$ | $2^{-1023} * 2^{-52} \approx 4.94 * 10^{−324}$ |
To be continued …