可能是因为简历里面写了个大大的 “计算机系统结构方向”，然后面的几个厂的岗位也都是偏系统方向，秋招面试的时候被好几个面试官都按在地上狂问系统方面的问题。

其中大概尤其与 Cache 有关的内容比较有代表性，于是准备根据几次回忆出来的自己和小伙伴遇到的面试题好好理一理 Cache 这块的内容。

Basic

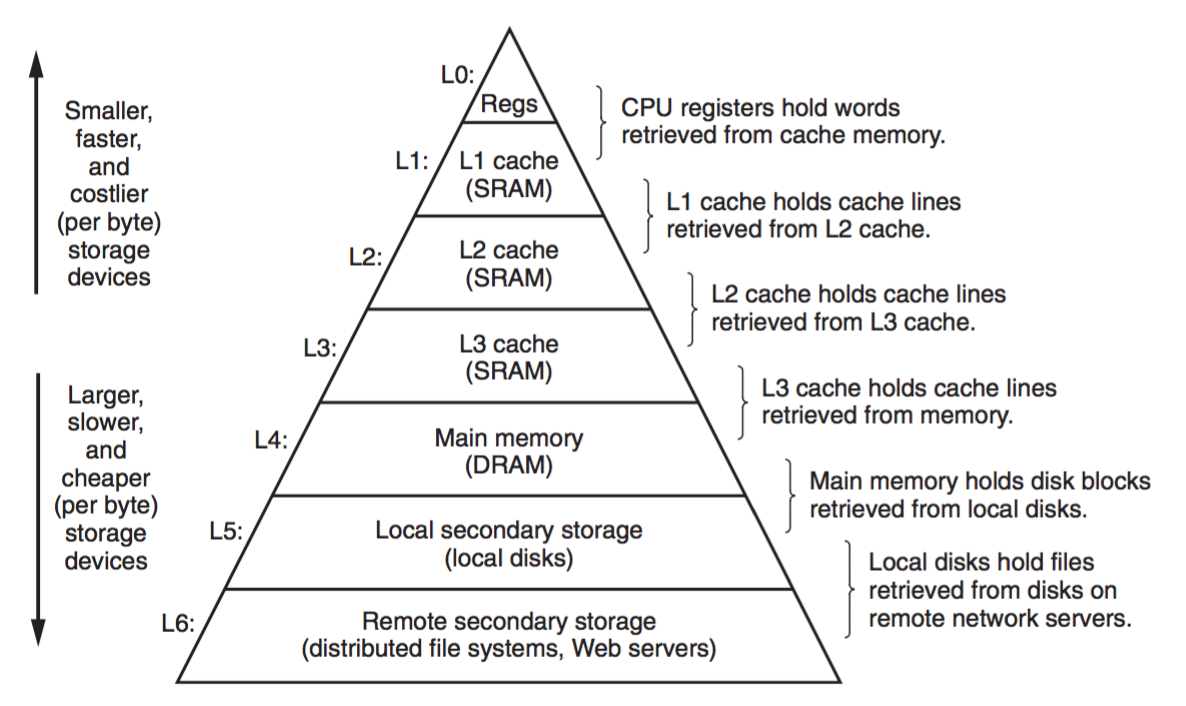
上图是一张最基础也最常见的存储器层次结构图，表达的是计算机系统中各级存储器的速度、容量、价格等等的金字塔关系。

Cache 这个思想本身特别简单，利用的核心原理就是数据的局部性，即把最常用到的东西放在最容易拿到的地方，这种局部性即包含了数据的空间局部性也包含了使用数据的时间局部性，但实际用起来效果却是非常地好，并且广泛应用在各种不同的场合中，例如：CPU 中的 Cache 用来加速对主存数据的访问，TLB 可以看成是对虚拟地址-物理地址转换的页表的 Cache，分布式环境中有的时候也会做个本地数据缓存，也是 Cache 的思想。

其实《硬软件接口》里面已经有介绍过 Cache 了，前面也有记过：

编程的时候 Cache 对程序员透明，写代码的人直接看到的是内存（……更准确地说看到的是虚拟的地址空间），但是 CPU 实际执行的时候访问的数据全部都是从 Cache 里面来的。每次访问一块新的内存数据时，首先检查 Cache 中是否存在，有就返回，没有就触发一次 Cache Miss，从主存把数据 load 到 Cache 中以后再返回。

然而 Cache 这个简单的想法在实际实现的时候可能会复杂的多，例如 Cache 分级，然后 Cache 还有多种数据和地址的映射关系，什么时候更新写回，地址冲突的时候怎么替换等等很多麻烦的问题都需要在实际实现的时候考虑。

这里还有两篇知乎上的小白科普文：

Interview Questions

面试的时候我和我的小伙伴们在 Cache 上踩了很多坑，虽然平时工作中很少有遇到需要考虑的这么深的，也就一般很少想到 Cache 这一层的工作内容了，但是终究说起来还是自己的基础没打扎实。

虚拟地址 or 物理地址？

L1 Cache 标记数据块用的是虚拟地址还是物理地址？

往后的 Cache 里面肯定用的是物理地址，这个没有任何悬念，关键在这个最靠近 CPU 的 L1 Cache 上。

这个问题一开始我脑子里冒出来的是当时看《硬软件接口》虚拟内存那章时画的那张图：CPU 先拿虚拟地址去查 TLB，然后再找 Cache，那妥妥的就是物理地址了。

后来一想这本书上是以一个假想的简单数据通路结构为例进行介绍，可能细节上后来有变动，然后去翻了下《量化》，里面没有详细讲，但是看图感觉像是用的虚拟地址。

再后来去网上搜这个问题的时候，说物理地址的也有，说虚拟地址的也有，还各有各的理由，于是就更迷了。

直到我在这个专栏文章中看到了这张图：

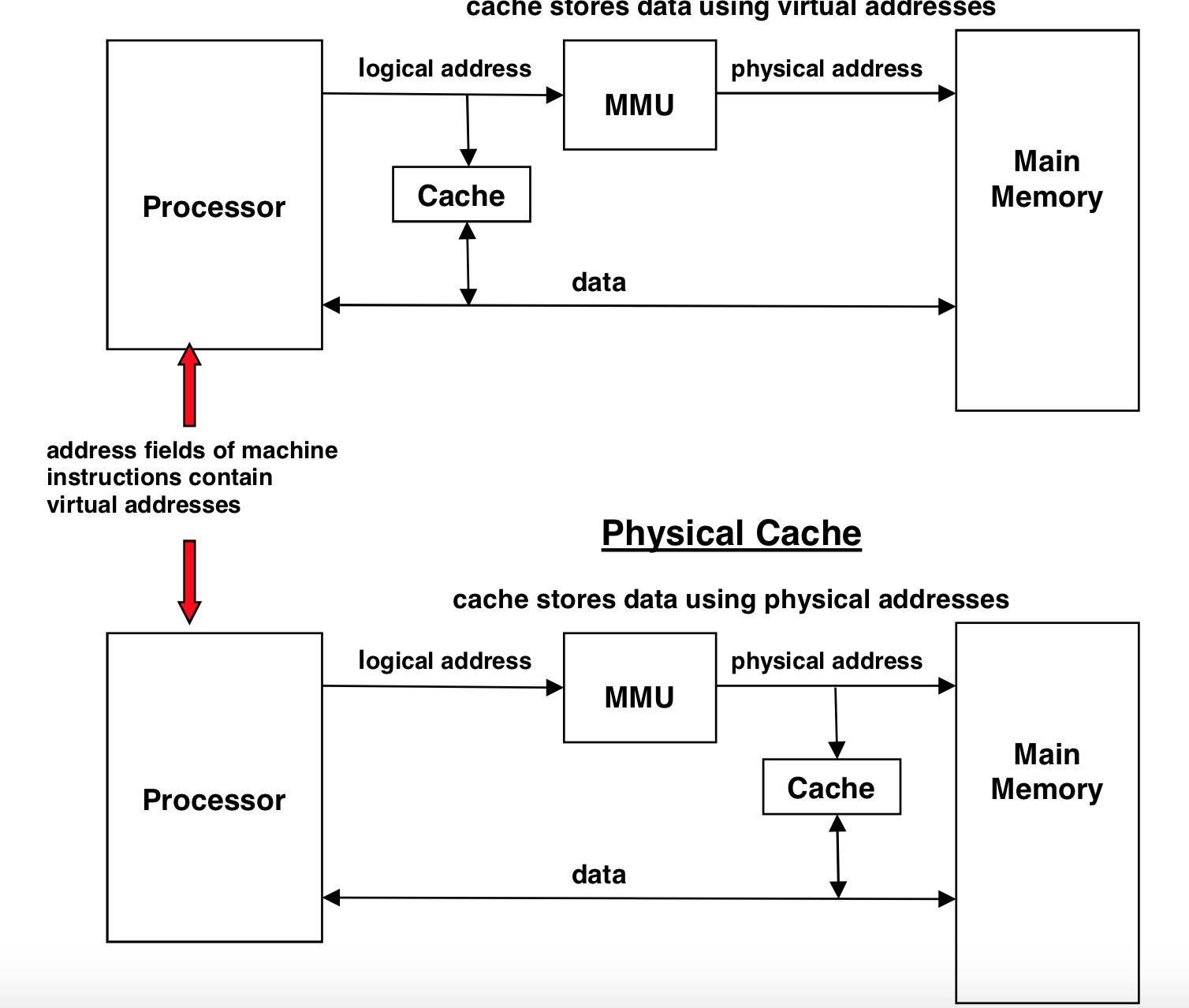
MMU 是 CPU 中用于虚拟地址-物理地址转换的工作单元（主要是页表、TLB 甚至多级 TLB 等等组成），这张图中根据芯片实际实现时 MMU 和 Cache 的位置关系，则很明显 L1 Cache 可能用虚拟地址也可能用物理地址了。

那我们来考虑一下这两种实现的区别：

Logical Cache/ Virtual Cache

感觉这种实现访问速度应该更快一点，因为不需要经过地址翻译就能够直接在 Cache 中搜索数据了。

问题是每个进程的虚拟地址空间都是独立的，如果有多个进程在同一个核上切换，则每次切换的时候都需要把 Cache 刷掉（话说我其实不太清楚这个代价会有多大，也不知道这个会不会成为制约性能的一个原因），当然，也有可能有多个虚拟地址对应到同一个物理地址上的这种情况，那这种情况要怎么处理就需要考虑更多东西了。

……真麻烦啊。
Physical Cache

查 Cache 前不管怎么样先把地址转换做了，这样前面 Logical Cache 存在的问题也就不存在了，而且也不需要一切换进程就刷一遍整个 L1 Cache，如果有多个虚拟地址对应到同一个物理地址上也无所谓。

问题大概就在于 MMU 的地址转换上，如果 TLB Miss 了，查页表还是要访问到主存上，那再查 Cache 就需要花更多的时间了。

CPU_cache 的维基百科页对地址转换这块也有大段篇幅的介绍。Cache 受地址转换影响在 Latency、Aliasing、Granularity 等几个方面都需要考虑到，根据用虚拟地址还是物理地址进行查找和标记，常见的也有下面四种 Cache 实现方式：

Physically Indexed, Physically Tagged(PIPT)

对应前面的 Physical Cache，没啥大毛病，就是慢
Virtually Indexed, Virtually Tagged(VIVT)

对应前面的 Logical Cache/ Virtual Cache，带来的麻烦问题很多
Virtually Indexed, Physically Tagged(VIPT)

可能是最好的一种实现方式了，目前市场上的一些现代处理器应该大多都是基于这种方式或者在这个基础上优化的。

由于查虚拟地址的索引和查 TLB 可以同时进行，这种方式的延迟会比 PIPT 低很多，但是实际数据还是要等到 MMU 把物理地址算出来之后对比 tag 才能确定。

另一方面由于用了物理地址作为 tag，VIVT 中可能会有的虚拟地址冲突的问题也解决了。
Physically Indexed, Virtually Tagged(PIVT)

这个…大概只会出现在文献中，实际实现的时候会集合 PIPT 和 VIVT 所有的缺点。

另外，对 Cache 数据的查找和标记还需要考虑到全相联、组相联等不同的映射关系的实现。

对 Cache 每一级的访存需要多少个 Cycle 有概念吗？

对 Context Switch 和 Cache 访存需要大概花费多少个 Cycle 有概念吗？

并没有……卒。

看一下网上找到的答案：

Register：1 Cycle
L1 Cache：3 Cycles
L2 Cache：10+ Cycles
L3 Cache：20~30+ Cycles
Main Memory：~100 Cycles

同样都是用 SRAM 做的，为什么会有速度差异呢？原因大概有以下几个：

容量大小

显而易见的是，Cache 的容量会随着级数的增加而增大。由于 Cache 需要做到随机访存，即能够直接访问到存储器的任意一个位置，在制程和设计完全一致的情况下，容量越大就需要花费更多的时间来做到随机访存（延迟跟容量的开方大致成正比）。
芯片上与 CPU 的距离

在芯片面积有限的情况下，L1 Cache 会被放置在离 CPU 核心非常近的地方，而 L2 Cache 就只能放到边缘位置了。

L1 中的指令 Cache 会在 Fetch 单元附近，数据 Cache 会在 Load/ Store 单元附近，L2 Cache 就要在 CPU 流水线外面了，L3 更远要在核外了。
具体实现的差异

L1 和 L2 在设计时的侧重点会有所区别，L1 更注重速度，而 L2 要在 L1 Miss 之后才发挥作用，因此更注重节能和容量。

查询一个地址时，L1 Cache 会把多个 Cache Line 的 tag 和数据全部取出来，然后再比较 tag 看哪一个命中或者都没命中。

而 L2 Cache 虽然也是 N 路组相联，但是比较时会先取 tag，当找到命中的之后再去把对应的数据取出来。

L3 做在核外，通常是多个核共享，因此还需要额外考虑一致性等等更多的东西。

关于 Context Switch 这点，进程和线程的切换其实都要涉及到上下文的切换。

进程切换时由于虚拟地址空间不同，因此需要切换页面映射、刷新 TLB 等等，如果是线程切换则开销会小很多。

为什么需要分级？

这个问题直接有别人解答了，感觉说的也还算清楚：

【Cache为什么有那么多级？为什么一级比一级大？是不是Cache越大越好？】

组成结构？

当时被问到这个问题的时候有点懵逼，不确定面试官想表达的是什么意思，我回答 “Index、tag、cache line data” 的时候被否决了……然后后来就没有答上来了。

如果指的不是全相联、组相联这种实现的话，可能想问的是硬件实现？

我对 Cache 硬件结构的了解就只是知道它是用 SRAM 做的，其他的就不懂了，卒。

这一块能够找到的资料也比较模糊，最后是从王齐的《浅谈 Cache Memory》中找到了比较靠谱的答案：

组相联方式组织的 Cache 会分成两个部分，Tag 部分和数据部分分开存放，例如一个 8 路组相联的 Cache 结构是这样的：

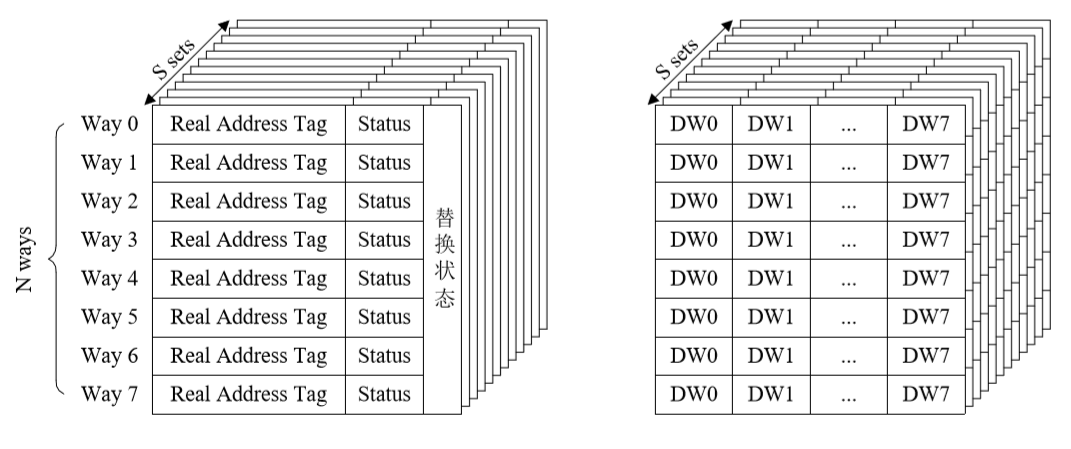
左边是地址 Tag 以及当前 Cache Line 的状态，右边是实际存放的数据。

这两类字段由于功能和特性不同，会使用两种不同类型的存储器来存放。Tag 阵列多使用 CAM（Content Addressable Memory）来存放，以利于并行查找，数据字段用的才是多端口多 Bank 的 SRAM。一般说的 Cache 大小也都指的是 SRAM 数据块的大小，CAM 这部分不包含在内。

CAM 对应的应该是前面结构图中一个 Set 中的多个 Way 的结构。首先根据需要访问的虚拟地址确定 Index 找到在哪个 Set 中，然后对该 Set 中的多条记录并行进行 Tag 的比对。

CAM 的基本结构如下：

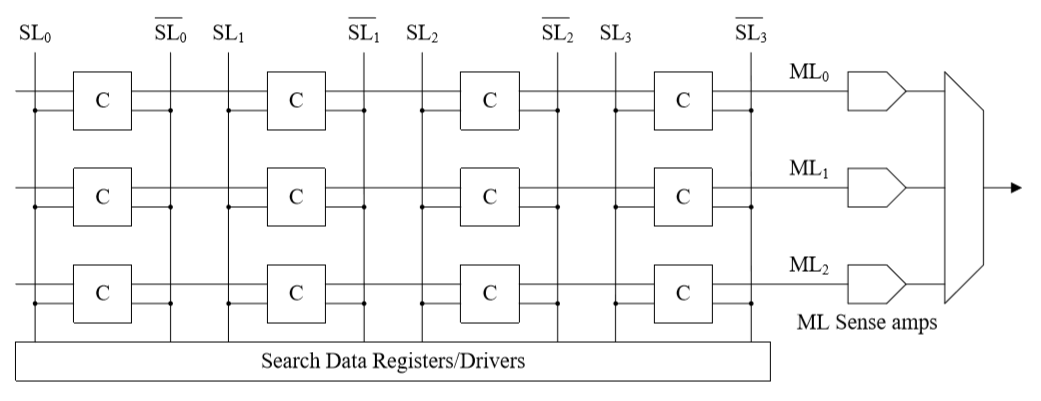
上图的 CAM 有 3 个 Word，分别对应一条横向的 ML（Match Line），每一个 Word 由 4 个 Bits （CAM Cell）组成。在每一列中，Bits 分别与两个 SL（Search Line）对应。

使用 CAM 进行查找时，首先需要把需要搜索的目标（Tag）放入 Search Data Register/Drivers 中，分解成多个 Bits 之后，通过 SL 发送到所有的 CAM Cell 中，每个 Cell 的 Hit/Miss 信息会向右传递给各自的 ML，最终 ML 汇总得到自己的 Hit/Miss 情况，这样就能够确定下来在当前的多个 Way 里面有没有命中的数据了。

后面更细节的就跳过了。

如何测出一块未知 CPU 的 Cache 参数？

假如你是一个 Intel 的工程师，有一天你的竞争对手 AMD 推出了一款新的 CPU，然后你想要知道关于其中的 Cache 的信息，要怎么做？没有其他任何的资料，只能通过实际测试的方式。

这个问题是紧接着上一个的，由于我被问到上一个问题的时候已经懵逼了，这题基本上完全没答上来，其实后来想想应该至少能把 Cache 的大小测出来，当时回答的时候真的是表现得太差了。

参考：

根据第一篇的程序稍微改了一下：

/* ***********************************************
MYID	: Chen Fan
LANG	: G++
PROG	: 
************************************************ */

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <sys/time.h>

using namespace std;

#define KB (1024/4)
#define MB (1024 * KB)
#define SIZE (128 * MB)

double getTime()
{
    struct timeval tv;
    gettimeofday(&tv, NULL);
    //获取秒
    double sec = (double)tv.tv_sec;
    //获取微秒
    double usec = (double)tv.tv_usec;
    //返回微秒数
    return sec * 1000000 + usec;
}

void cache_line_test(int *array)
{
    for (int stride=1;stride<64*KB;stride*=2)
    {
        double begin_time = getTime();
        for (int i=0;i<SIZE;i+=stride)
        {
            array[i] *= 10;
        }
        double end_time = getTime();
        printf("Stride: %5d,  Line Size: %5d Bytes,  Average Cost: %10lf us\n", stride, stride*4, (end_time - begin_time) / (SIZE/stride));
    }
}

void cache_block_test(int *array)
{
    for (int num=KB;num<MB;num*=2)
    {
        int len = num-1;
        int tot = SIZE-1;
        double begin_time = getTime();
        for (int i=0;i<tot;i++)
        {
            array[(i*16) & len] *= 10;
        }
        double end_time = getTime();
        printf("Num: %8d,  Size: %8d KB,  cost %10lf us\n", num, num*4/1024, end_time - begin_time);
    }
    for (int num=MB;num<16*MB;num+=MB)
    {
        int len = num-1;
        int tot = SIZE-1;
        double begin_time = getTime();
        for (int i=0;i<tot;i++)
        {
            array[(i*16) & len] *= 10;
        }
        double end_time = getTime();
        printf("Num: %8d,  Size: %8d MB,  cost %10lf us\n", num, num*4/1024/1024, end_time - begin_time);
    }
}

int main()
{
    int *array = new int[SIZE];
    for (int i=0;i<SIZE;i++) array[i] = i;

    cache_line_test(array);
    cache_block_test(array);
    
    return 0;
}

结果：

Stride:     1,  Line Size:     4 Bytes,  Average Cost:   0.002586 us
Stride:     2,  Line Size:     8 Bytes,  Average Cost:   0.002613 us
Stride:     4,  Line Size:    16 Bytes,  Average Cost:   0.002622 us
Stride:     8,  Line Size:    32 Bytes,  Average Cost:   0.003078 us
Stride:    16,  Line Size:    64 Bytes,  Average Cost:   0.004280 us
Stride:    32,  Line Size:   128 Bytes,  Average Cost:   0.011414 us
Stride:    64,  Line Size:   256 Bytes,  Average Cost:   0.011412 us
Stride:   128,  Line Size:   512 Bytes,  Average Cost:   0.007610 us
Stride:   256,  Line Size:  1024 Bytes,  Average Cost:   0.015221 us
Stride:   512,  Line Size:  2048 Bytes,  Average Cost:   0.015732 us
Stride:  1024,  Line Size:  4096 Bytes,  Average Cost:   0.000000 us
Stride:  2048,  Line Size:  8192 Bytes,  Average Cost:   0.000000 us
Stride:  4096,  Line Size: 16384 Bytes,  Average Cost:   0.000000 us
Stride:  8192,  Line Size: 32768 Bytes,  Average Cost:   0.000000 us
Num:      256,  Size:        1 KB,  cost 86789.000000 us
Num:      512,  Size:        2 KB,  cost 88739.000000 us
Num:     1024,  Size:        4 KB,  cost 86736.000000 us
Num:     2048,  Size:        8 KB,  cost 91756.000000 us
Num:     4096,  Size:       16 KB,  cost 88762.000000 us
Num:     8192,  Size:       32 KB,  cost 94745.000000 us
Num:    16384,  Size:       64 KB,  cost 95744.000000 us
Num:    32768,  Size:      128 KB,  cost 105752.000000 us
Num:    65536,  Size:      256 KB,  cost 105684.000000 us
Num:   131072,  Size:      512 KB,  cost 108742.000000 us
Num:   262144,  Size:        1 MB,  cost 99733.000000 us
Num:   524288,  Size:        2 MB,  cost 114694.000000 us
Num:   786432,  Size:        3 MB,  cost 100699.000000 us
Num:  1048576,  Size:        4 MB,  cost 130651.000000 us
Num:  1310720,  Size:        5 MB,  cost 99732.000000 us
Num:  1572864,  Size:        6 MB,  cost 120678.000000 us
Num:  1835008,  Size:        7 MB,  cost 118715.000000 us
Num:  2097152,  Size:        8 MB,  cost 151562.000000 us
Num:  2359296,  Size:        9 MB,  cost 96772.000000 us
Num:  2621440,  Size:       10 MB,  cost 104690.000000 us
Num:  2883584,  Size:       11 MB,  cost 104754.000000 us
Num:  3145728,  Size:       12 MB,  cost 152557.000000 us
Num:  3407872,  Size:       13 MB,  cost 105716.000000 us
Num:  3670016,  Size:       14 MB,  cost 156583.000000 us
Num:  3932160,  Size:       15 MB,  cost 141678.000000 us

我笔记本是 i7 7700HQ，在网上可以查到详细的 Cache 信息

Cache:	L1 data	L1 instruction	L2	L3
Size:	4 x 32 KB	4 x 32 KB	4 x 256 KB	6 MB
Associativity:	8-way set associative	8-way set associative	4-way set associative	12-way set associative
Line size:	64 bytes	64 bytes	64 bytes	64 bytes
Comments:	Direct-mapped	Direct-mapped	Non-inclusive Direct-mapped	Inclusive Shared between all cores

Cache Line 比较好测，上面的代码中可以明显看到从 64 Bytes 开始，平均访问时间出现跳变。

L1、L2、L3 各自的大小……说实话我觉得这样测效果并不好，变化倒是确实有，就是其中可能还有很多误差成分在。

CSAPP 上面讲 Cache 的那章用的是类似的方法，根据这样的测试结果可以画出一张“存储器山”的图。

多核情况下 Cache 会有什么问题？

这个问的主要应该就是 Cache 的一致性、写回、写直达等等这些方面的内容。

另外还有一个叫做伪共享（False Sharing）的问题：

多核 CPU 通常都是 L1、L2 每个核独立，共享 L3。如上图这种情况，两个核实际操作的数据是独立的，但是它们恰好在一个 Cache Line 里面，则其中一个作了修改之后，另一个的 Cache Line 也会跟着失效，引起了本来不必要的效率问题。

Chenfan Blog

（试图）深入理解 Cache