正好复习信号到FFT了,想起来前段时间放了挺久的FFT大数乘法,顺便研究下。
普通的高精度乘法的复杂度需要$O(n^2)$,用了押位之后,一般押4位的话能够达到$O(n^2/16)$,看上去可能效果不错,但仍然是同一个数量级的。
对付更大一点的变态数据(。。。ACM赛场上很少有卡这货的吧。。。-_-////)就需要用的$O(nlogn)$的FFT大数乘法算法了。
数学基础
首先基础是DFT,FFT是DFT的一种快速算法。
从N点DFT出发:
$$
\begin{align}
X[K] &= \sum_{n=0}^{N-1}x[n]e^{-j\frac{2\pi K}{N}n} \\
&=\sum_{n=0}^{\frac{N}{2}-1}x[2n]e^{-j\frac{2\pi K}{N}2n}+\sum_{n=0}^{\frac{N}{2}-1}x[2n+1]e^{-j\frac{2\pi K}{N}(2n+1)} \\
&=\sum_{n=0}^{\frac{N}{2}-1}x_1[n]e^{-j\frac{2\pi K}{\frac{N}{2}}n}+\sum_{n=0}^{\frac{N}{2}-1}x_2[n]e^{-j\frac{2\pi K}{\frac{N}{2}}n}e^{-j\frac{2\pi K}{N}} \\
&=X_1[K]+e^{-j\frac{2\pi K}{N}}X_2[K]
\end{align}
$$
也就是说,通过上述变换,我们成功地将一个N点得DFT拆成了2个$\frac{N}{2}$点的DFT
分析一下复杂度:
首先N点DFT的结果$X[K]$有N点,每个点的计算都要对$x[n]$的n个序列值乘上负指数求和,复杂度是$O(n^2)$
如果每一步都采用上面的那种变换方式,那么可以把多出来的一维降掉,变成$O(nlogn)$,这也就是快速傅里叶变换(FFT)了!
更进一步
然而上面这个式子简化到最后是有问题的。
我们把一个N点的DFT拆成$\frac{N}{2}$点的DFT之后,下面得到的两个序列$X_1[K]$和$X_2[K]$都只有$\frac{N}{2}$点。
也就是说直接这么写,当K大于$\frac{N}{2}-1$之后,放在代码里面,后面部分就会出现数组越界的问题!!
继续分析后面部分:
$$
\begin{align}
X_1[K]&=\sum_{n=0}^{\frac{N}{2}-1}x_1[n]e^{-j\frac{2\pi K}{\frac{N}{2}}n} \\
X_1[\frac{N}{2}+K]&=\sum_{n=0}^{\frac{N}{2}-1}x_1[n]e^{-j\frac{2\pi}{\frac{N}{2}}(\frac{N}{2}+K)n}\\
&=\sum_{n=0}^{\frac{N}{2}-1}x_1[n]e^{-j\frac{2\pi K}{\frac{N}{2}}n}e^{-j2\pi n}\\
&=-\sum_{n=0}^{\frac{N}{2}-1}x_1[n]e^{-j\frac{2\pi K}{\frac{N}{2}}n}\\
&=X_1[K]
\end{align}
$$
好,这样问题就解决了。
令:
$$W_N^K=e^{-j\frac{2\pi K}{N}}$$
则重新整理上面的运算单元可以得到:

这就是著名的蝶形运算了。
然后整个图画出来是这样的:
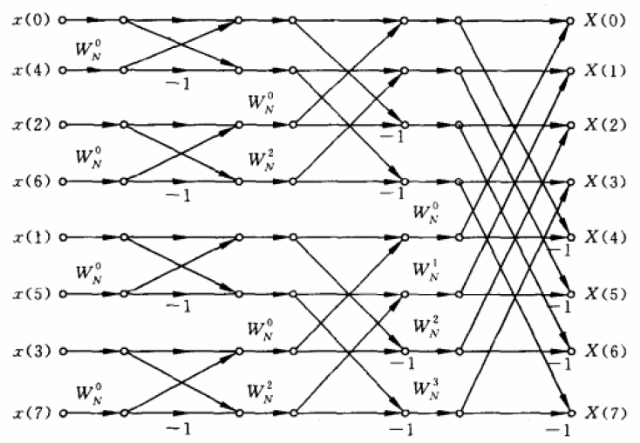
8点FFT
或者:
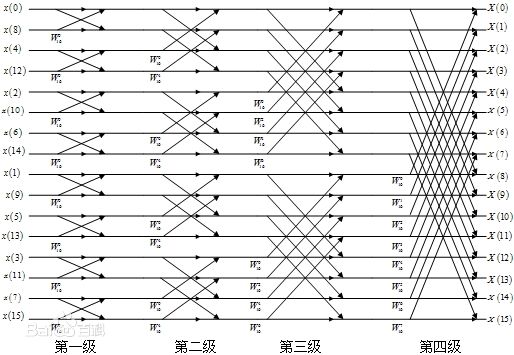
16点FFT
FFT的用途
综上,FFT就是专门为计算机快速运算而设计的,1点变2点,2点变4点,4点变8点……这样就能在原始数据(原数组)的基础上不断计算下一层的结果,最终完成整个DFT的快速计算。
写代码的话,第一步是处理一下最左边一排原始数据的摆放顺序,是按照二进制逆序排过来的,然后一层一层求和迭代即可。
多项式
讲完FFT之后,下面重点来了。
多项式的系数表示法
关于变量$x$的多项式可以表示成:
$$A(x)=a_0+a_1x+a_2x^2+…+a_{n-1}x^{n-1}=\sum_{j=0}^{n-1}a_jx^j$$
多项式是个广泛的概念,如果把大数对应到多项式上面去那就是类似这样:
$$1234=4+3*10+2*10^2+1*10^3$$
若有:
$$B(x)=\sum_{j=0}^{n-1}b_jx^j$$
则:
$$A(x)+B(x)\Rightarrow C(x)=\sum_{j=0}^{n-1}c_jx^j$$
$$c_j=a_j+b_j$$
$$A(x)\cdot B(x)\Rightarrow C(x)=\sum_{j=0}^{2n-2}c_jx^j$$
$$c_j=\sum_{k=0}^{j}a_kb_{j-k}$$
分别是多项式加法和多项式乘法
注意:多项式乘法的过程就是多项式系数卷积
多项式的点值表示法
令:
$$y_k=A(x_k)$$
则一个次数界为n的多项式$A(x)$的点值表示就是n个这样的点值(任意n个)对所形成的集合:
$$\{(x_0,y_0),(x_1,y_1),…,(x_{n-1},y_{n-1})\}$$
从系数表示法写成点值表示法就是简单地说找n个不同的$x$代进去求出$y$,然后写在一起就行了。
然而用点值确定系数就是个线性求解的过程,称为插值,也是可以算的。
那么点值表示法有什么好处呢?
设上面的点值表示是$A(x)$的,如果已知$B(x)$的是:
$$\{(x_0,y’_0),(x_1,y’_1),…,(x_{n-1},y’_{n-1})\}$$
那么:
$$A(x)+B(x)\Rightarrow C(x)=\{(x_0,y_0+y’_0),(x_1,y_1+y’_1),…,(x_{n-1},y_{n-1}+y’_{n-1})\}$$
$$A(x)\cdot B(x)\Rightarrow C(x)=\{(x_0,y_0y’_0),(x_1,y_1y’_1),…,(x_{n-1},y_{n-1}y’_{n-1})\}$$
分别是多项式加法和多项式乘法
关键在于,这里的多项式乘法的复杂度是$O(n)$!!!!!
因此只要能够想办法快速地进行两种表示法之间的转换,那么就可以先从系数表示法转换成点值表示法,用$O(n)$相乘之后,再快速转换回去,即可做到快速的多项式相乘
所以!!!!
转换的关键就是!!!!
FFT!!!!
以下是多项式乘法的过程:
- 次数界增加一倍:通过加入n个值为0的高阶系数,将整个次数界扩充至$2n$
- 求值,两次FFT分别求出$A(x)$和$B(x)$的长度为$2n$的点值表示$A(\omega)$和$B(\omega)$
- 逐个相乘得到$C(\omega)$
- 再做一次FFT,求逆傅里叶变换得到$C(x)$
实现代码详见模板题:HDU 1402 A * B Problem Plus 快速高精度乘法(FFT)