Size Balanced Tree

这将会是你踏入高级数据结构的第一步。

终于要开始给队里面讲这种比较高级的数据结构了，也趁此机会自己好好理理。

首先要讲的是这个：

二叉搜索树

---

二叉搜索树又叫二叉排序树，它的定义很简单：

1. 这是一棵二叉树

2. 令x为二叉树中某个结点上表示的值，那么其左子树上所有结点的值都要不大于x，其右子树上所有结点的值都要不小于x

存储结构一般用链表或者结构体数组模拟链表等等均可。

中序遍历二叉排序树可得到一个关键字的有序序列，一个无序序列可以通过构造一棵二叉排序树变成一个有序序列，构造树的过程也可以看成是对无序序列进行排序的过程。

基本操作有几种：

• 插入

每次插入的新的结点都是二叉排序树上新的叶子结点，在进行插入操作时，不必移动其它结点，只需改动某个结点的指针，由空变为非空即可。

• 查找

根据查找值的大小与当前子树的根节点相比，更小就找左边，更大就找右边，知道找到目标或者返回无结果。

• 子树中的最大/最小值

从根开始走到最左边是最小，走到最右边是最大。

• 前驱或后继

查找比当前点小的最大值（前驱）或比当前点更大的最小值（后继）。考虑左子树的最大值和右子树的最小值，若没有左右子树则考虑父节点。

• 删除

删除的第一步是要先找到该节点，然后在子树中找个前驱或者后继来替换掉该结点即可。

搜索，插入，删除的复杂度等于树高，因此一般的操作都是O(logn)的。

思想其实很简单，具体的实现就不贴代码了，因为确实也比较简单。

普通的二叉搜索树存在的问题

---

！！！树高并不稳定！！！
或者说，不平衡

考虑一组本来就有序的数列，将其插入二叉搜索树，结果就是二叉树会退化成一条链，所有结点只有右子树，左子树是空的。

因而预期的O(logn)的操作会退化成O(n)，数据稍大点这种结构就悲剧了。

为了解决这个问题，机智的人类想出了改进方案：

平衡树

---

平衡树是在二叉查找树的基础上，增加维护操作，使得二叉查找树保持左右子树平衡，以最大限度地保证整体的效率。这种结构就叫做平衡树。

当然，维护也是需要消耗时间的，一般来说维护消耗的时间越长，树越平衡。具体的还要看实际情况。

一般常见的平衡树有不少种：红黑树、AVL树、SBT、Treap、Splay等等。

它们的基本思想都是通过结点的左右旋来保持原本二叉搜索树的性质不变，然后高效完成。区别就是保持平衡的方式不同。

比如红黑树是把结点分成红黑两种，然后各种旋转稳定，貌似效率相当高，然而实现比较麻烦。

Treap是用优先级的思想，在树上加上堆($Treap=Tree+Heap$)。

相比起来Splay比较特殊，Splay其实并不是一棵严格意义上的平衡树，因为它的操作并不是主要为了保证左右平衡的，它的特点主要是结构比较灵活，可以用来处理一些正常平衡树完成不了的问题，缺点就是常数大，效率可能不高。嗯，这是后话。

今天的重点是这个：

SBT

---

节点大小平衡树(Size Balanced Tree)是一种自平衡二叉查找树。

它是由中国广东中山纪念中学的**陈启峰**（也是个神人，本来那年拿到了北美地区的ACM冠军，结果封神之路上遇到了Watashi）发明的。陈启峰于2006年底完成论文《[Size Balanced Tree](http://jcf94.com/download/2015-06-19-sbt-Qifeng-Chen《Size Balanced Tree》.pdf)》，并在2007年的全国青少年信息学奥林匹克竞赛冬令营中发表。

相比红黑树、AVL树等自平衡二叉查找树，SBT更易于实现。据陈启峰在论文中称，SBT是“目前为止速度最快的高级二叉搜索树”。

旋转

首先是所有平衡树中都会用到的旋转操作，平衡树需要不断改变树的结构，但是改变结构的同时又必须保证的是整棵树的二叉查找树性质不能被破坏掉（要是二叉查找树性质都没了，下面就不用玩了）。

调整方式就是逐点进行左旋或者右旋：

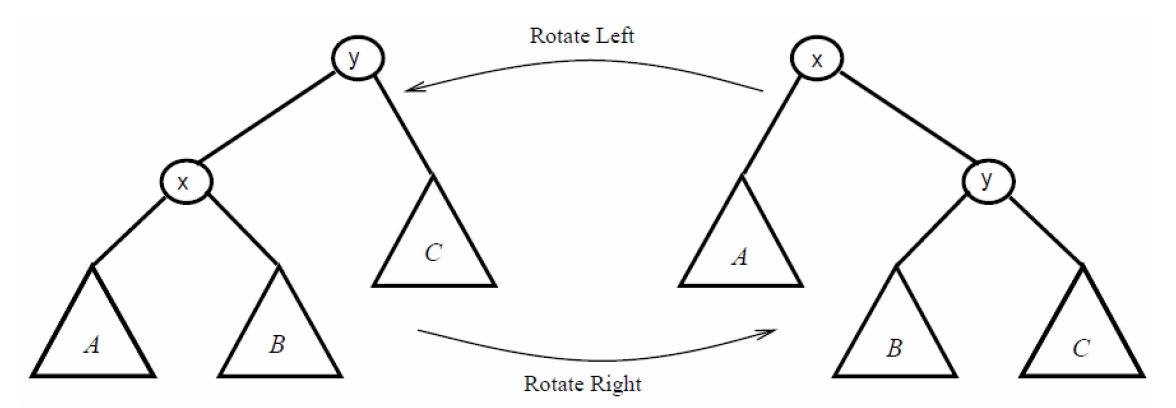
以上图作为例子，左右旋实现起来其实也很简单，就是交换一下x、y的父子关系，然后调整B子树的连接情况，且能够保证整体的二叉搜素性质不改变。

SBT的特殊性质

我们给二叉搜索树的结点增加一个size域，用来保存以该节点为根的子树中一共有多少个结点。

上面说了，SBT是通过结点大小(Size)来调整整棵树的平衡性的，它相比一般的二叉搜索树多出来的性质有两条：

对于SBT中的每一个结点t，有：

1. $size[right[t]]>=size[left[left[t]]],size[right[left[t]]]$

2. $size[left[t]]>=size[left[right[t]]],size[right[right[t]]]$

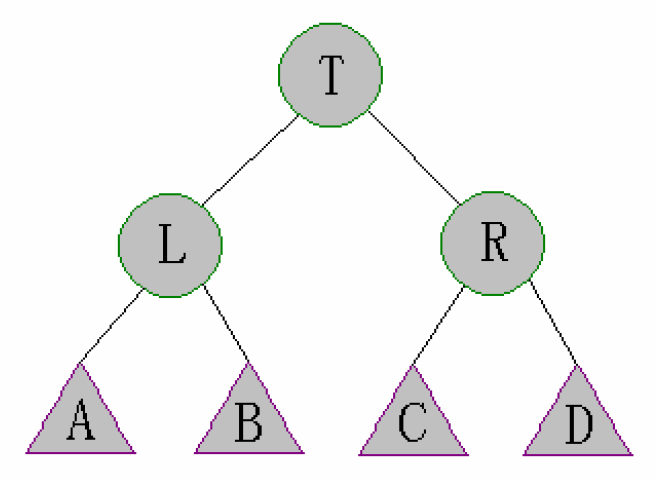
以上图为例，性质是：

1. $size[R]>=size[A]$
2. $size[R]>=size[B]$
3. $size[L]>=size[C]$
4. $size[L]>=size[D]$

如何维护这种性质？Maintain(& t)

为了便于说明，以下部分左右旋与Maintain函数的参数传递均为实参

我们从上图开始，把整棵树的结构分成几种情况来看：

Case 1：size[left[left[t]]]>size[right[t]]

• 首先对t进行右旋，此时t更新成了原图中的L

得到如下的结果：

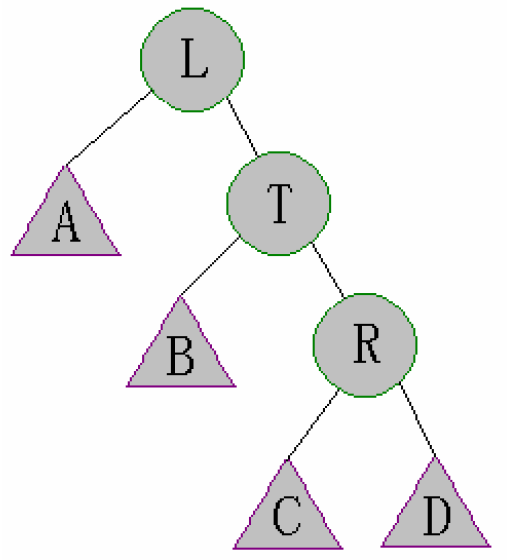
• 则对于图中的T，其子树不一定满足性质，需要Maintain(T)

• 当T调整完之后，T的子树与L可能也不一定满足性质，需要再次Maintain(L)

该过程的伪代码为：

If size[left[left[t]]]>size[right[t]] then
	Right-Rotate(t)
	Maintain(right[t])
	Maintain(t)

Case 2: size[right[left[t]]]>size[right[t]]

这种情况要稍微复杂一些：

我们把原图中的B再往下画一层：

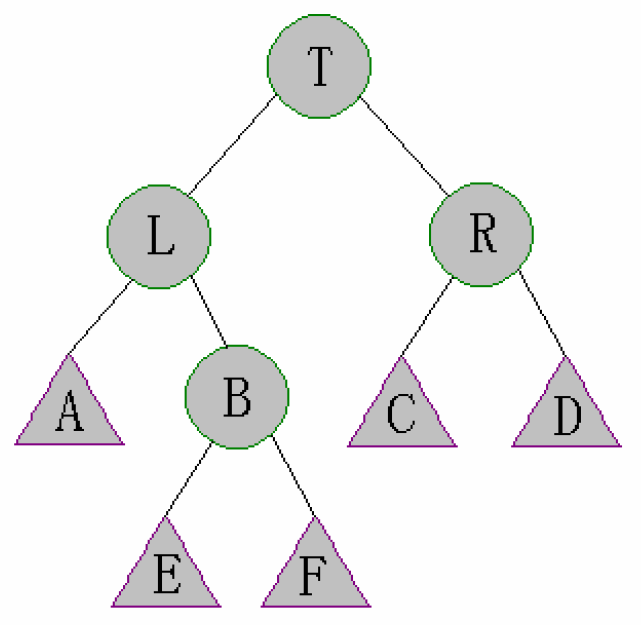
• 首先对L进行左旋

得到：

• 再右旋T

得到：

• 经过上面两步操作之后，整棵树的结构可以说是完全改变了，具体形态也可能变得难以预测。但是根据左右旋的性质，我们可以保证上图的结果中A、E、F、R都是性质完好的SBT，所以只要分别Maintain(L)和Maintain(T)即可。

• 经过上面那一步，我们能保证L和T以及其子树都是性质完好了，但是它们之间的任然不能确保，所以需要再Maintain(B)一次

该过程的伪代码：

If s[right[left[t]]>s[right[t]] then
	Left-Rotate(left[t])
	Right-Rotate(t)
	Maintain(left[t])
	Maintain(right[t])
	Maintain(t)

Case 3: size[right[right[t]]]>size[left[t]]

情况与第一种类似，刚好相反

Case 4: size[left[right[t]]]>size[left[t]]

情况与第二种类似，刚好相反

总结

按照上述说明，Maintain函数就是四个if语句分开即可，但是中间可能会有一些不必要的操作，故作者在[论文]((http://jcf94.com/download/2015-06-19-sbt-Qifeng-Chen《Size Balanced Tree》.pdf))中也对其进行了改进。

可以发现1、2与3、4的判断是可以分开的，于是可以添加一个标记参数，已确定接下来的Maintain中需要检查哪一边

改进之后的伪代码：

Maintain (t,flag)
	If flag=false then
		If size[left[left[t]]]>size[right[t]] then
			Right-Rotate(t)
		Elseif size[right[left[t]]>size[right[t]] then
			Left-Rotate(left[t])
			Right-Rotate(t)
		Else exit
	Elseif size[right[right[t]]]>size[left[t]] then
    	Left-Rotate(t)
	Elseif size[left[right[t]]]>size[left[t]] then
		Right-Rotate(right[t])
		Left-Rotate(t)
    Else exit

    Maintain(left[t],false)
    Maintain(right[t],true)
    Maintain(t,false)
    Maintain(t,true)

愉快地使用SBT

SBT的核心操作是Maintain，经过上面这么多内容，我想你已经掌握了。

SBT支持所有普通二叉查找树的操作（显而易见），而有了Maintain，之后所有的操作都是在普通的二叉查找树的基础上加以改进即可，可以衍生出更多有用的操作。

• 插入

正常的二叉查找树插入操作，插入完之后Maintain维护性质

• 删除

直接使用正常的二叉查找树删除操作即可。

你说SBT性质可能会被破坏？

嗯，是的。确实可能会出现这种情况，然而平衡树的操作是为了是的树的平均深度的平衡性。对于删除来说，删除一个结点并不会增加树的深度，所以在这里不用Maintain对整体并不会有什么影响，下次其他操作的Maintain就可以修复这个问题了。

• 查找

与正常的二叉查找树相同

• 查找第k大

由于每个结点的Size域，我们可以快速找出整个数列中第k大的数。根结点是第size[左子树]+1小的数，所以从根结点出发，按照大小关系不断遍历左右子树即可。

复杂度也是O(logn)的。

最终代码示例

这份模板是我自己改过好多遍的，当初学这个的时候特别痛苦。网站找的别人的模板要不就有问题，要不就写得让人觉得很难受。然后找到的几个人的模板还都不一样，参考都累。

最后自己在纸上推左右旋推了很久才定下来，后来做题的时候又改进过好多遍。

推荐大家多画图。。。

/* ***********************************************
MYID	: Chen Fan
LANG	: G++
PROG	: Size Balanced Tree
************************************************ */

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

#define MAXN 100010

int sons[MAXN][2];
int size[MAXN],data[MAXN];
int sbt=0,sbttail=0;

void rotate(int &t,int w) //rotate(&node,0/1)
{
	int k=sons[t][1-w];
	if (!k) return ;
	sons[t][1-w]=sons[k][w];
	sons[k][w]=t;
	size[k]=size[t];
	size[t]=size[sons[t][0]]+size[sons[t][1]]+1;
	t=k;
}

void maintain(int& t,bool flag) //maintain(&node,flag)
{
	if (!t) return ;
	if (!flag)
		if (size[sons[sons[t][0]][0]]>size[sons[t][1]]) rotate(t,1);
		else if (size[sons[sons[t][0]][1]]>size[sons[t][1]]) 
		{
			rotate(sons[t][0],0);
			rotate(t,1);
		} else return ;
	else
		if (size[sons[sons[t][1]][1]]>size[sons[t][0]]) rotate(t,0);
		else if (size[sons[sons[t][1]][0]]>size[sons[t][0]])
		{
			rotate(sons[t][1],1);
			rotate(t,0);
		} else return ;
	
	maintain(sons[t][0],false);
	maintain(sons[t][1],true);
	maintain(t,false);
	maintain(t,true);
}

void insert(int& t,int v,int pos) //insert(&root,value,pos/0)
{
	if (!size[t])
	{
		if (!pos)
		{
			sbttail++;
			pos=sbttail;
		}
		data[pos]=v;
		size[pos]=1;
		sons[pos][0]=0;
		sons[pos][1]=0;
		t=pos;
	} else 
	{
		size[t]++;
		if (v<data[t]) insert(sons[t][0],v,pos);
		else insert(sons[t][1],v,pos);
		maintain(t,v>=data[t]);
	}
}

int last; //last node
int del(int& t,int v) //value=del(&root,key)
{
	size[t]--;
	if (v==data[t]||(v<data[t]&&sons[t][0]==0)||(v>data[t]&&sons[t][1]==0))
	{
		int ret=data[t];
		if (sons[t][0]==0||sons[t][1]==0) 
		{
			last=t;
			t=sons[t][1]+sons[t][0];
		}
		else data[t]=del(sons[t][0],data[t]+1);
		return ret;
	} else
	if (v<data[t]) return del(sons[t][0],v);
	else return del(sons[t][1],v);
}

int delk(int& t,int k) //value=del(&root,k)
{
	size[t]--;
	if (size[sons[t][0]]+1==k)
	{
		int ret=data[t];
		if (sons[t][0]==0||sons[t][1]==0) 
		{
			last=t;
			t=sons[t][1]+sons[t][0];
		}
		else data[t]=delk(sons[t][0],data[t]+1);
		return ret;
	} else
	if (k<=size[sons[t][0]]) return delk(sons[t][0],k);
	else return delk(sons[t][1],k-1-size[sons[t][0]]);
}

int select(int t,int k) //node=select(root,k)
{
	if (k==size[sons[t][0]]+1) return t;
	if (k<=size[sons[t][0]]) return select(sons[t][0],k);
	else return select(sons[t][1],k-1-size[sons[t][0]]);
}

int search(int t,int x) //node=search(root,x)
{
	if (t==0||x==data[t]) return t;
	if (x<data[t]) return search(sons[t][0],x);
	else return search(sons[t][1],x);
}

void deb_out()
{
	printf("-------\n");
	printf("sbttail=%d sbt=%d\n",sbttail,sbt);
	for	(int i=1;i<=sbttail;i++)
	printf("%2d: key=%2d size=%2d left=%2d right=%2d\n",i,data[i],size[i],sons[i][0],sons[i][1]);
	printf("-------\n");
}

int main()
{
	sbttail=0;
	sbt=0;
	
	for	(int i=1;i<=15;i++) insert(sbt,i,0);
	deb_out();
	
	//printf("%d\n",del(sbt,8));
	insert(sbt,8,0);
	deb_out();
	del(sbt,8);
	del(sbt,8);
	//printf("%d\n",search(sbt,8));
	deb_out();
}

后话

SBT可以用来快速维护一组数的插入、查找、删除、找第k大，然而你会发现只是想要单纯地实现这个功能，C++ STL 中的set就可以做到。哦对了，set不能找第k大……

事实上set里面就是用红黑树来进行维护的。。。
然而我并不会红黑树。。。
然而你们也并不需要会红黑树。。。
因为直接用set就好了啊。。。-_-///
不用set那么用SBT嘛，这种东西学一个就差不多了

所以虽然SBT效率高，但是扩展性似乎并没有特别强，一般需要用到的也就是只有动态多次求第k的时候。

真正想要见识一下神器的，请在未来好好研究学习Treap和Splay吧，这两个在应用的时候比SBT的用途广很多。

如需要模板题练手，请点击页面下方的标签查看详情。

当然模板可以参考，不过还是不要复制粘贴代码了，最好能自己写一遍。