Chenfan Blog

Do cool things that matter.

0%

HDU 2475 BOX 动态树 Link-Cut Tree

Posted on Edited on In

Box

Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)

Problem Description

There are N boxes on the ground, which are labeled by numbers from 1 to N. The boxes are magical, the size of each one can be enlarged or reduced arbitrarily. Jack can perform the “MOVE x y” operation to the boxes: take out box x; if y = 0, put it on the ground; Otherwise, put it inside box y. All the boxes inside box x remain the same. It is possible that an operation is illegal, that is, if box y is contained (directly or indirectly) by box x, or if y is equal to x. In the following picture, box 2 and 4 are directly inside box 6, box 3 is directly inside box 4, box 5 is directly inside box 1, box 1 and 6 are on the ground.

1

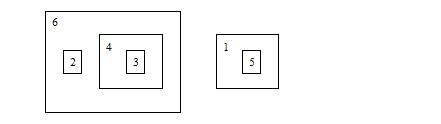
The picture below shows the state after Jack performs “MOVE 4 1”:

2

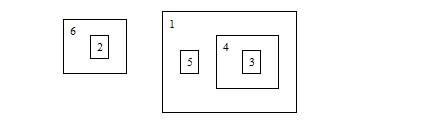
Then he performs “MOVE 3 0”, the state becomes:

3

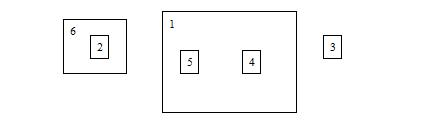
During a sequence of MOVE operations, Jack wants to know the root box of a specified box. The root box of box x is defined as the most outside box which contains box x. In the last picture, the root box of box 5 is box 1, and box 3’s root box is itself.

Input

Input contains several test cases. For each test case, the first line has an integer N (1 <= N <= 50000), representing the number of boxes. Next line has N integers: a1, a2, a3, … , aN (0 <= ai <= N), describing the initial state of the boxes. If ai is 0, box i is on the ground, it is not contained by any box; Otherwise, box i is directly inside box ai. It is guaranteed that the input state is always correct (No loop exists). Next line has an integer M (1 <= M <= 100000), representing the number of MOVE operations and queries. On the next M lines, each line contains a MOVE operation or a query:

  1. MOVE x y, 1 <= x <= N, 0 <= y <= N, which is described above. If an operation is illegal, just ignore it.

  2. QUERY x, 1 <= x <= N, output the root box of box x.

Output

For each query, output the result on a single line. Use a blank line to separate each test case.

Sample Input

2
0 1
5
QUERY 1
QUERY 2
MOVE 2 0
MOVE 1 2
QUERY 1
6
0 6 4 6 1 0
4
MOVE 4 1
QUERY 3
MOVE 1 4
QUERY 1

Sample Output

1
1
2

1
1

题意

动态地维护一些盒子套盒子的操作，询问根。

分析

盒子与盒子的关系可以直观地用树的结构来表示，一个结点下的子结点可以表示大盒子里面直接套着的小盒子。

所以本题就是一个裸的Link-Cut Tree模型了。

关于LCT树，还是推荐Yang Zhe的QTREE论文吧。

动态树是用访问操作来划分树链，对于每一条树链，使用Splay来维护，用深度作为splay的左右关系。

看了很多代码，觉得还是写不好，总觉得别人的用起来不顺，最后是在自己原来Splay的基础上改的。

原本的整棵树是个splay，但是在LCT中，整棵树是由很多棵分散的Splay组合起来的，于是在其中的一些点上加上root标记，表示以这一点为根下面可以形成一棵splay树。多个这样的splay组合完成之后就是一棵LCT了。

后面的代码中加入了输入输出挂。。。。。。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
/* ***********************************************
MYID    : Chen Fan
LANG    : G++
PROG    : HDU 2475
************************************************ */

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

#define MAXN 50010

int sons[MAXN][2];
int father[MAXN],pathfather[MAXN],data[MAXN];
bool root[MAXN];
int spttail=0;

void rotate(int x,int w) //rotate(node,0/1)
{
    int y=father[x];
    
    sons[y][!w]=sons[x][w];
    if (sons[x][w]) father[sons[x][w]]=y;
    father[x]=father[y];
    if (father[y]&&(!root[y])) sons[father[y]][y==sons[father[y]][1]]=x;
    sons[x][w]=y;
    father[y]=x;

    if (root[y])
    {
        root[x]=true;
        root[y]=false;
    }
}

void splay(int x) //splay(node)
{
    while(!root[x])
    {
        if (root[father[x]]) rotate(x,x==sons[father[x]][0]);
        else 
        {
            int t=father[x];
            int w=(sons[father[t]][0]==t);
            if (sons[t][w]==x)
            {
                rotate(x,!w);
                rotate(x,w);
            } else 
            {
                rotate(t,w);
                rotate(x,w);
            }
        }
    }
}

void access(int v)
{
    int u=v;
    v=0;
    while(u)
    {
        splay(u);
        root[sons[u][1]]=true;
        sons[u][1]=v;
        root[v]=false;
        v=u;
        u=father[u];
    }
}

int findroot(int v)
{
    access(v);
    splay(v);
    while (sons[v][0]) v=sons[v][0];
    //splay(v,0);
    return v;
}

void cut(int v)
{
    access(v);
    splay(v);
    father[sons[v][0]]=0;
    root[sons[v][0]]=true;
    sons[v][0]=0;
}

void join(int v,int w)
{
    if (!w) cut(v);
    else 
    {
        access(w);
        splay(w);
        int temp=v;
        while(!root[temp]) temp=father[temp];
        if (temp!=w)
        {
            cut(v);
            father[v]=w;
        }
    }
}

int INT() 
{
    char ch;
    int res;
    while (ch=getchar(),!isdigit(ch));
    for (res = ch - '0';ch = getchar(),isdigit(ch);)
        res = res * 10 + ch - '0';
    return res;
}

char CHAR() 
{
    char ch, res;
    while (res = getchar(), !isalpha(res));
    while (ch = getchar(), isalpha(ch));
    return res;
}

int main()
{
    //freopen("2475.txt","r",stdin);
    
    int n;
    double flag=false;
    while(scanf("%d",&n)!=EOF)
    {
        if (flag) printf("\n");
        flag=true;

        memset(father,0,sizeof(father));
        memset(sons,0,sizeof(sons));
        for (int i=1;i<=n;i++) 
        {
            //scanf("%d",&father[i]);
            father[i]=INT();
            root[i]=true;
        }

        int m;
        m=INT();
        for (int i=1;i<=m;i++)
        {
            char s=CHAR();
            if (s=='M')
            {
                int x,y;
                x=INT();
                y=INT();
                join(x,y);
            } else 
            {
                int q;
                q=INT();
                printf("%d\n",findroot(q));
            }
        }
    }

    return 0;
}
Related Posts