Chenfan Blog

Do cool things that matter.

0%

The 2014 ACM-ICPC Asia Regional Anshan

Posted on Edited on In

继续复盘下一场Regional！

【A】-_-///

【B】模拟（之前每次遇到模拟、暴搜都直接跳了，题目太长也是一个原因…下次是在不行可以尝试一下）

【C】数论 互质、容斥？

【D】数学推导（方差）+贪心

【E】签到DP

【F】-_-///

【G】最小割的灵活运用

【H】搜索+打表

【I】签到题

【J】-_-///

【K】计算几何、置换群（Polya计数）

【L】AC自动机+树链剖分

D、HDU 5073 Galaxy

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)

Special Judge

Problem Description

Good news for us: to release the financial pressure, the government started selling galaxies and we can buy them from now on! The first one who bought a galaxy was Tianming Yun and he gave it to Xin Cheng as a present.

1

To be fashionable, DRD also bought himself a galaxy. He named it Rho Galaxy. There are n stars in Rho Galaxy, and they have the same weight, namely one unit weight, and a negligible volume. They initially lie in a line rotating around their center of mass.

Everything runs well except one thing. DRD thinks that the galaxy rotates too slow. As we know, to increase the angular speed with the same angular momentum, we have to decrease the moment of inertia.

The moment of inertia I of a set of n stars can be calculated with the formula

2

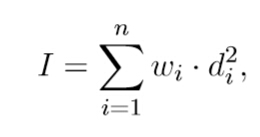
where wi is the weight of star i, di is the distance form star i to the mass of center.

As DRD’s friend, ATM, who bought M78 Galaxy, wants to help him. ATM creates some black holes and white holes so that he can transport stars in a negligible time. After transportation, the n stars will also rotate around their new center of mass. Due to financial pressure, ATM can only transport at most k stars. Since volumes of the stars are negligible, two or more stars can be transported to the same position.

Now, you are supposed to calculate the minimum moment of inertia after transportation.

Input

The first line contains an integer T (T ≤ 10), denoting the number of the test cases.

For each test case, the first line contains two integers, n(1 ≤ n ≤ 50000) and k(0 ≤ k ≤ n), as mentioned above. The next line contains n integers representing the positions of the stars. The absolute values of positions will be no more than 50000.

Output

For each test case, output one real number in one line representing the minimum moment of inertia. Your answer will be considered correct if and only if its absolute or relative error is less than 1e-9.

Sample Input

2
3 2
-1 0 1
4 2
-2 -1 1 2

Sample Output

0
0.5

题意

平面中有n个点，最多可以移动k个点，使原题条件中的I达到最小值。物理题，计算转动惯量。

分析

开始的时候真是死活看不懂题……

原题中的wi始终为1，即可忽略，然后di指的是x距离所有点重心的距离，这里的重心即是所有点坐标的平均值了。所以原式可以写成这样：

3

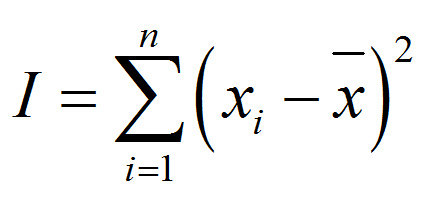
分析一下这个东西跟方差很像，所以可以写成：

4

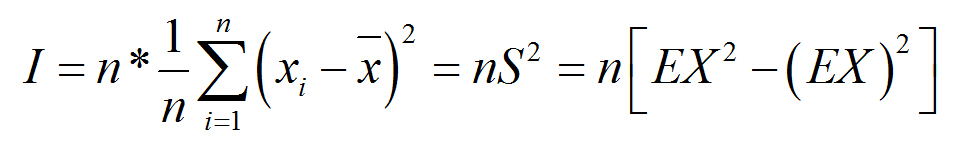
然后：

5

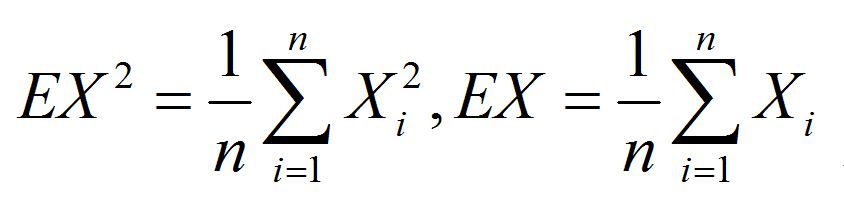
最后：

6

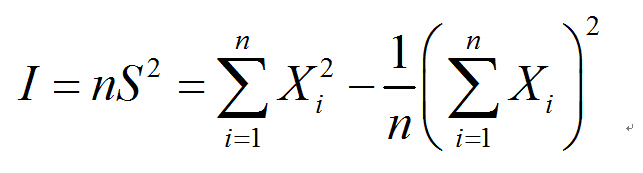
基本的I的计算方法就推导出来了，接下来是k的问题。

为了让I尽可能的小，也就是让方差尽可能的小，那么最佳的方案就是把距离重心最远的k个点都移到重心去。则首先根据坐标排序，从两端开始枚举取数，前面取i个那最后就取k-i个，找到一种最佳的取数方案把最外围的点都移掉即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
/* ***********************************************
MYID    : Chen Fan
LANG    : G++
PROG    : HDU 5073
************************************************ */

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

long long a[50010],sum[50010],sum2[50010];

int main()
{
    int t;
    scanf("%d",&t);
    for (int tt=1;tt<=t;tt++)
    {
        int n,k;
        scanf("%d%d",&n,&k);

        for (int i=1;i<=n;i++) scanf("%lld",&a[i]);

        if (n==k)
        {
            printf("0\n");
            continue;
        }

        sort(&a[1],&a[n+1]);
        memset(sum,0,sizeof(sum));
        memset(sum2,0,sizeof(sum2));
        for (int i=1;i<=n;i++)
        {
            sum[i]=sum[i-1]+a[i];
            sum2[i]=sum2[i-1]+a[i]*a[i];
        }
        
        double mi=sum2[n-k]-(double)sum[n-k]*sum[n-k]/(n-k);
        for (int i=1;i<=k;i++)
        {
            double temp=sum2[n-k+i]-sum2[i]-(double)(sum[n-k+i]-sum[i])*(sum[n-k+i]-sum[i])/(n-k);
            if (mi>temp) mi=temp;
        }

        printf("%.10f\n",mi);
    }

    return 0;
}

杭电上%lld和%I64d老是出问题…%lld提交通不过的话改成%I64d应该就可以了

E、HDU 5074 Hatsune Miku

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)

Problem Description

Hatsune Miku is a popular virtual singer. It is very popular in both Japan and China. Basically it is a computer software that allows you to compose a song on your own using the vocal package.

Today you want to compose a song, which is just a sequence of notes. There are only m different notes provided in the package. And you want to make a song with n notes.

7

Also, you know that there is a system to evaluate the beautifulness of a song. For each two consecutive notes a and b, if b comes after a, then the beautifulness for these two notes is evaluated as score(a, b).

So the total beautifulness for a song consisting of notes a1, a2, . . . , an, is simply the sum of score(ai, ai+1) for 1 ≤ i ≤ n - 1.

Now, you find that at some positions, the notes have to be some specific ones, but at other positions you can decide what notes to use. You want to maximize your song’s beautifulness. What is the maximum beautifulness you can achieve?

Input

The first line contains an integer T (T ≤ 10), denoting the number of the test cases.

For each test case, the first line contains two integers n(1 ≤ n ≤ 100) and m(1 ≤ m ≤ 50) as mentioned above. Then m lines follow, each of them consisting of m space-separated integers, the j-th integer in the i-th line for score(i, j)( 0 ≤ score(i, j) ≤ 100). The next line contains n integers, a1, a2, . . . , an (-1 ≤ ai ≤ m, ai ≠ 0), where positive integers stand for the notes you cannot change, while negative integers are what you can replace with arbitrary notes. The notes are named from 1 to m.

Output

For each test case, output the answer in one line.

Sample Input

2
5 3
83 86 77
15 93 35
86 92 49
3 3 3 1 2
10 5
36 11 68 67 29
82 30 62 23 67
35 29 2 22 58
69 67 93 56 11
42 29 73 21 19
-1 -1 5 -1 4 -1 -1 -1 4 -1

Sample Output

270
625

分析

简单的签到DP，f(i,j)表示摆到第i个符号，且最后一个取j的最大分数，则f(i,j)=max(f(i-1,k)+score(k,j))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
/* ***********************************************
MYID    : Chen Fan
LANG    : G++
PROG    : HDU 5074
************************************************ */

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

int a[110];
int f[110][60];
int score[60][60];

int main()
{
    int t;
    scanf("%d",&t);
    for (int tt=1;tt<=t;tt++)
    {
        int n,m;
        scanf("%d%d",&n,&m);

        memset(score,0,sizeof(score));
        for (int i=1;i<=m;i++)
        for (int j=1;j<=m;j++) scanf("%d",&score[i][j]);

        for (int i=1;i<=n;i++) scanf("%d",&a[i]);

        memset(f,0,sizeof(f));
        for (int i=2;i<=n;i++)
        {
            if (a[i]>0)
                if (a[i-1]>0) f[i][a[i]]=f[i-1][a[i-1]]+score[a[i-1]][a[i]];
                else for (int j=1;j<=m;j++)
                    f[i][a[i]]=max(f[i][a[i]],f[i-1][j]+score[j][a[i]]);
            else 
                if (a[i-1]>0) 
                    for (int j=1;j<=m;j++) f[i][j]=f[i-1][a[i-1]]+score[a[i-1]][j];
                else for (int j=1;j<=m;j++)
                        for (int k=1;k<=m;k++) f[i][j]=max(f[i][j],f[i-1][k]+score[k][j]);
        }

        if (a[n]>0) printf("%d\n",f[n][a[n]]);
        else 
        {
            int ma=0;
            for (int i=1;i<=m;i++)
            if (ma<f[n][i]) ma=f[n][i];
            printf("%d\n",ma);
        }
    }

    return 0;
}

I、HDU 5078 Osu!

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)

Special Judge

Problem Description

Osu! is a very popular music game. Basically, it is a game about clicking. Some points will appear on the screen at some time, and you have to click them at a correct time.

8

Now, you want to write an algorithm to estimate how diffecult a game is.

To simplify the things, in a game consisting of N points, point i will occur at time ti at place (xi, yi), and you should click it exactly at ti at (xi, yi). That means you should move your cursor from point i to point i+1. This movement is called a jump, and the difficulty of a jump is just the distance between point i and point i+1 divided by the time between ti and ti+1. And the difficulty of a game is simply the difficulty of the most difficult jump in the game.

Now, given a description of a game, please calculate its difficulty.

Input

The first line contains an integer T (T ≤ 10), denoting the number of the test cases.

For each test case, the first line contains an integer N (2 ≤ N ≤ 1000) denoting the number of the points in the game. Then N lines follow, the i-th line consisting of 3 space-separated integers, ti(0 ≤ ti < ti+1 ≤ 106), xi, and yi (0 ≤ xi, yi ≤ 106) as mentioned above.

Output

For each test case, output the answer in one line.

Your answer will be considered correct if and only if its absolute or relative error is less than 1e-9.

Sample Input

2
5
2 1 9
3 7 2
5 9 0
6 6 3
7 6 0
10
11 35 67
23 2 29
29 58 22
30 67 69
36 56 93
62 42 11
67 73 29
68 19 21
72 37 84
82 24 98

Sample Output

9.2195444573
54.5893762558

分析

签到题，唯一要注意的是数据范围，两个1e6数量级的数相乘有超int的可能。

Related Posts