Chenfan Blog

Do cool things that matter.

0%

The 2014 ACMICPC Asia Regional Shanghai Online

Posted on Edited on In

XorZip小队第一次合作，虽然结果还是有些可惜，但是状态和感觉都还不错。

【A】数论+二分（-_-///）

【B】Lucas定理+数位DP（-_-///）

【C】LCA、LCT+树链剖分

【D】题目分解成DP+状态压缩

【E】DLX（-_-///）

【F】推算公式+大数

【G】几何题，线段与椭球的交点

【H】Kuangbin说这是个简单DP（简单…0.0…）矩阵优化

【I】GCD+大数

【J】本福特定律（妈蛋，这是个啥？……）

【K】LCT

【L】签到题

D、Contest

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)

Problem Description

In the ACM International Collegiate Programming Contest, each team consist of three students. And the teams are given 5 hours to solve between 8 and 12 programming problems.

On Mars, there is programming contest, too. Each team consist of N students. The teams are given M hours to solve M programming problems. Each team can use only one computer, but they can’t cooperate to solve a problem. At the beginning of the ith hour, they will get the ith programming problem. They must choose a student to solve this problem and others go out to have a rest. The chosen student will spend an hour time to program this problem. At the end of this hour, he must submit his program. This program is then run on test data and can’t modify any more.

Now, you have to help a team to find a strategy to maximize the expected number of correctly solved problems.

For each problem, each student has a certain probability that correct solve. If the ith student solve the jth problem, the probability of correct solve is Pij .

At any time, the different between any two students’ programming time is not more than 1 hour. For example, if there are 3 students and there are 5 problems. The strategy {1,2,3,1,2}, {1,3,2,2,3} or {2,1,3,3,1} are all legal. But {1,1,3,2,3},{3,1,3,1,2} and {1,2,3,1,1} are all illegal.

You should find a strategy to maximize the expected number of correctly solved problems, if you have know all probability

Input

The first line of the input is T (1 ≤ T ≤ 20), which stands for the number of test cases you need to solve.

The first line of each case contains two integers N ,M (1 ≤ N ≤ 10,1 ≤ M ≤ 1000),denoting the number of students and programming problem, respectively.

The next N lines, each lines contains M real numbers between 0 and 1 , the jth number in the ith line is Pij .

Output

For each test case, print a line “Case #t: ”(without quotes, t means the index of the test case) at the beginning. Then a single real number means the maximal expected number of correctly solved problems if this team follow the best strategy, to five digits after the decimal point. Look at the output for sample input for details.

Sample Input

1
2 3
0.6 0.3 0.4
0.3 0.7 0.9

Sample Output

Case #1: 2.20000

题意

这是另一个次元的ACM比赛么…0.0…每个队伍N个人，一共M道题，每小时一题，每题限定只能有1人做题，其他人出去玩。给出每个队员对每一道题解出的概率，最后要求计算出一种方案，使得最终的出题数数学期望最大化。

分析

初看感觉是个贪心啊，但是文中有一句当时困扰了比赛N多队伍的描述：

At any time, the different between any two students’ programming time is not more than 1 hour.

后面还有个让人摸不着头脑的sample，顿时好多童鞋表示看不懂。

额，这句话的意思是队伍中所有成员的做题数必须平均，不能出现一名队员比另外一名队员多做1题以上的情况，简单地说就是必须要等所有成员都做过1题之后，才能有人继续做第2个题。

这样思路就不难想出来了：

N的上限是10，则把M按照N个一组分开，每一组都要求每个人选择一题，使得总和最大。相当于一个N*N的矩阵，每行每列取一个数使得总和最大。

想明白之后顺手直接分组，DFS搜了一遍交上去，果然TLE。于是明白了，这个要用状态压缩的DP来解。

对于每一组：

f(i,j)表示第i题，j状态时达到的最大和，j用一个最大为2^10的数来表示每个人在当前组是否有做过题目的状态
则：
f(i,j)=max{f(i-1,j-1<<k)+a[k][i]} j&(1<<k)==(1<<k)

想明白方程之后就是分组细节上的处理了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
/* ***********************************************
MYID    : Chen Fan
LANG    : G++
PROG    : D1004
************************************************ */

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

int po[]={1,2,4,8,16,32,64,128,256,512,1024,2048};
double a[20][1010];
bool flag[20];
double f[20][2000];
int n;

double doit(int l,int r,double sum)
{
    memset(f,0,sizeof(f));
    for (int i=1;i<=r-l+1;i++)
    for (int j=0;j<=po[n]-1;j++)
    {
        double temp=0;
        for (int k=0;k<n;k++)
        if (((1<<k)&j-(1<<k))==0)
        if (temp<f[i-1][j-(1<<k)]+a[k+1][l+i-1]) temp=f[i-1][j-(1<<k)]+a[k+1][l+i-1];
        f[i][j]=temp;
    }
    
    return f[r-l+1][po[n]-1];
}

int main()
{
    int t;
    scanf("%d",&t);
    for (int tt=1;tt<=t;tt++)
    {
        int m;
        scanf("%d%d",&n,&m);
        for (int i=1;i<=n;i++)
        for (int j=1;j<=m;j++) scanf("%lf",&a[i][j]);
        
        double ans=0;
        int t1=m/n;
        for (int i=1;i<=t1;i++)
        {
            double temp=doit((i-1)*n+1,i*n,0);
            ans+=temp;
        }
        double temp=doit(t1*n+1,m,0);
        ans+=temp;
        
        printf("Case #%d: %.5f\n",tt,ans);
    }
    return 0;
}

启发

有些题目可能局部是满足DP性质的，可以分解一下再做DP。

F、Sawtooth

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)

Problem Description

Think about a plane:

  • One straight line can divide a plane into two regions.
  • Two lines can divide a plane into at most four regions.
  • Three lines can divide a plane into at most seven regions.
  • And so on…

Now we have some figure constructed with two parallel rays in the same direction, joined by two straight segments. It looks like a character “M”. You are given N such “M”s. What is the maximum number of regions that these “M”s can divide a plane ?

pic

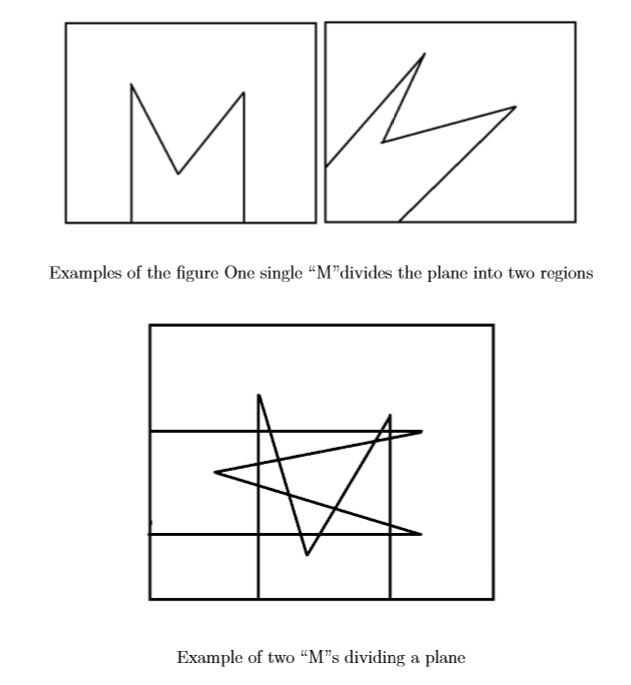
Input

The first line of the input is T (1 ≤ T ≤ 100000), which stands for the number of test cases you need to solve.

Each case contains one single non-negative integer, indicating number of “M”s. (0 ≤ N ≤ 1012)

Output

For each test case, print a line “Case #t: ”(without quotes, t means the index of the test case) at the beginning. Then an integer that is the maximum number of regions N the “M” figures can divide.

Sample Input

2
1
2

Sample Output

Case #1: 2
Case #2: 19

题意

在平面上摆上M，摆上一个的时候能把平面分成2个部分，摆上2个的时候能分成19个部分，求摆上n个的时候能分成多少个部分。

分析

这样的题目首先能想到的肯定是通过公式推算完成，但是由两组数据还很难推出公式，于是我们艰难地画出了第三个M，最后数出来是52。

经过一番艰难地推算，算出来了公式是ans=8n^2-7n+1。

开始感觉估算出来long long是足够大的，交了一次没过，以为是公式问题，，，后来才发现10^12平方之后早就爆了64位了，于是转用大数。

比赛时用了JAVA，TLE，然后之前又没有自己准备C的大数模板，悲剧收场…

JAVA

队友整理了个好用的JAVA模板，这玩意以前还不怎么会，经过这次之后应该是没问题了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
/* ***********************************************
MYID    : Chen Fan
LANG    : JAVA
PROG    : HDU5047
************************************************ */

import java.io.*;
import java.math.BigInteger;
import java.util.*;

public class Main 
{
    static PrintWriter out=new PrintWriter(new BufferedWriter(
        new OutputStreamWriter(System.out)));

    public static void main(String[] args) throws IOException
    {
        Scan scan=new Scan();

        int t=scan.nextInt();
        for (int tt=1;tt<=t;tt++) 
        {
            String s=scan.next();
            BigInteger a=new BigInteger(s);
            a=a.multiply(BigInteger.valueOf(8)).multiply(a).subtract(a.multiply(BigInteger.valueOf(7))).add(BigInteger.valueOf(1));
            out.printf("Case #%d: ",tt);
            out.println(a);
        }

        out.flush();
    }
}

class Scan 
{
    BufferedReader buffer;
    StringTokenizer tok;

    Scan() 
    {
        buffer=new BufferedReader(new InputStreamReader(System.in));
    }

    boolean hasNext() 
    {
        while (tok==null||!tok.hasMoreElements())
        {
            try
            {
                tok=new StringTokenizer(buffer.readLine());
            } catch (Exception e)
            {
                return false;
            }
        }
        return true;
    }

    String next()
    {
        if (hasNext()) return tok.nextToken();
        return null;
    }

    int nextInt()
    {
        return Integer.parseInt(next());
    }
}

不用JAVA

其实最终的结果没有超出long long太多，当时比赛的时候脑子没转过来，用两个long long的变量把结果分成两部分完全就能存下来了-_-////哭死，这个思路就是简化版的大数操作。

I、Divided Land

Time Limit: 8000/4000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)

Problem Description

It’s time to fight the local despots and redistribute the land. There is a rectangular piece of land granted from the government, whose length and width are both in binary form. As the mayor, you must segment the land into multiple squares of equal size for the villagers. What are required is there must be no any waste and each single segmented square land has as large area as possible. The width of the segmented square land is also binary.

Input

The first line of the input is T (1 ≤ T ≤ 100), which stands for the number of test cases you need to solve.

Each case contains two binary number represents the length L and the width W of given land. (0 < L, W ≤ 21000)

Output

For each test case, print a line “Case #t: ”(without quotes, t means the index of the test case) at the beginning. Then one number means the largest width of land that can be divided from input data. And it will be show in binary. Do not have any useless number or space.

Sample Input

3
10 100
100 110
10010 1100

Sample Output

Case #1: 10
Case #2: 10
Case #3: 110

题意

给出一块平面，要求使用一些正方形去摆满，求最大正方形的边长。

分析

首先要想到正方形分矩形的最大边长是其长和宽的最大公约数。

然后就是计算二进制（大数）的最大公约数的问题了。

很不好意思的是，JAVA中也是直接有模板可以套用的，而且借由快速的输入输出模板，题目变得so easy了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
/* ***********************************************
MYID    : Chen Fan
LANG    : JAVA
PROG    : HDU5050
************************************************ */

import java.io.*;
import java.math.BigInteger;
import java.util.*;

public class Main 
{
    static PrintWriter out=new PrintWriter(new BufferedWriter(
            new OutputStreamWriter(System.out)));

    public static void main(String[] args) throws IOException 
    {
        Scan scan=new Scan();

        int t=scan.nextInt();

        for (int tt=1;tt<=t;tt++)
        {
            String s=scan.next();
            BigInteger a=new BigInteger(s,2);
            s=scan.next();
            BigInteger b=new BigInteger(s,2);
            out.printf("Case #%d: ",tt);
            out.println(a.gcd(b).toString(2));
        }

        out.flush();
    }
}

class Scan 
{

    BufferedReader buffer;
    StringTokenizer tok;

    Scan() 
    {
        buffer=new BufferedReader(new InputStreamReader(System.in));
    }

    boolean hasNext() 
    {
        while (tok==null||!tok.hasMoreElements()) 
        {
            try 
            {
                tok=new StringTokenizer(buffer.readLine());
            } catch (Exception e) 
            {
                return false;
            }
        }
        return true;
    }

    String next() 
    {
        if (hasNext()) return tok.nextToken();
        return null;
    }
    int nextInt() 
    {
        return Integer.parseInt(next());
    }
}

L、the Sum of Cube

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)

Problem Description

A range is given, the begin and the end are both integers. You should sum the cube of all the integers in the range.

Input

The first line of the input is T(1 <= T <= 1000), which stands for the number of test cases you need to solve. Each case of input is a pair of integer A,B(0 < A <= B <= 10000),representing the range[A,B].

Output

For each test case, print a line “Case #t: ”(without quotes, t means the index of the test case) at the beginning. Then output the answer – sum the cube of all the integers in the range.

Sample Input

2
1 3
2 5

Sample Output

Case #1: 36
Case #2: 224

分析

求a~b的立方和，防止爆零。

Related Posts