Chenfan Blog

Do cool things that matter.

0%

HDU 2489 Minimal Ratio Tree 最小生成树+DFS

Posted on Edited on In

Minimal Ratio Tree

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)

Problem Description

For a tree, which nodes and edges are all weighted, the ratio of it is calculated according to the following equation.

1

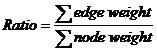
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.

2

Input

Input contains multiple test cases. The first line of each test case contains two integers n (2<=n<=15) and m (2<=m<=n), which stands for the number of nodes in the graph and the number of nodes in the minimal ratio tree. Two zeros end the input. The next line contains n numbers which stand for the weight of each node. The following n lines contain a diagonally symmetrical n×n connectivity matrix with each element shows the weight of the edge connecting one node with another. Of course, the diagonal will be all 0, since there is no edge connecting a node with itself.

All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].
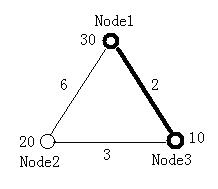
The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.

Output

For each test case output one line contains a sequence of the m nodes which constructs the minimal ratio tree. Nodes should be arranged in ascending order. If there are several such sequences, pick the one which has the smallest node number; if there’s a tie, look at the second smallest node number, etc. Please note that the nodes are numbered from 1 .

Sample Input

3 2
30 20 10
0 6 2
6 0 3
2 3 0
2 2
1 1
0 2
2 0
0 0

Sample Output

1 3
1 2

题意

给出一张n个点的图，图中的每一个结点以及每一条边都有其权值，要求从中选出m个点，找到m-1条边将其连接，使得边权值与点权值的比值达到最小。

分析

要使得比值最小，则点权值和尽可能地大同时边权值和尽可能地小。直接上考虑，边权值和尽可能小即对这m个点作最小生成树。

而题目给定的n不大，故可以用DFS搜出需要的m个点，然后对m个点进行最小生成树，中间注意判断和保存即可。

我用了一个dijkstra+优先队列的prim去找MST，这也是我第一次尝试使用STL的优先队列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>

using namespace std;

bool flag[16],outp[16];
int n,m,node[16];
int ma[16][16];
double mi;

typedef struct heaptyp
{
    int num,key;
    friend bool operator < (heaptyp a,heaptyp b)
    {
        return a.num>b.num;
    }
} heaptype;

void prim(int s,int tot)
{
    int i,j,now,ans;
    bool fla[16];
    priority_queue<heaptype>heap;
    heaptype aaa;
    
    memset(fla,0,sizeof(fla));
    fla[s]=true;
    ans=0;
    for (i=1;i<=n;i++) 
    if (flag[i]&&ma[s][i])
    {
        heaptype temp;
        temp.num=ma[s][i];
        temp.key=i;
        heap.push(temp);
        aaa=heap.top();
    }
    
    for (j=1;j<m;j++)
    {
        heaptype h=heap.top();
        heap.pop();
        aaa=heap.top();
        while (fla[h.key])
        {
            h=heap.top();
            heap.pop();
        }
        now=h.key;
        fla[now]=true;
        ans+=h.num;
        for (i=1;i<=n;i++)
        if (flag[i]&&ma[now][i])
        if (!fla[i])
        {
            heaptype temp;
            temp.num=ma[now][i];
            temp.key=i;
            heap.push(temp);
            aaa=heap.top();
        }
    }
    double rat=(double)ans/tot;
    if (mi-rat>0.0000001)
    {
        mi=rat;
        for (int i=1;i<=n;i++) outp[i]=fla[i];
    }
}

void dfs(int now,int last,int tot)
{
     if (now==m)
     {
         int i;
         for (i=1;i<=n;i++)
         if (flag[i]) break;
         prim(i,tot);
     }
     else 
     {
         now++;
         for (int i=last+1;i<=n-m+now;i++)
         {
             flag[i]=true;
             dfs(now,i,tot+node[i]);
             flag[i]=false;
         }
     }
}

int main()
{
    scanf("%d%d",&n,&m);
    while (!(n==0&&m==0))
    {
        for (int i=1;i<=n;i++) scanf("%d",&node[i]);
        for (int i=1;i<=n;i++)
        for (int j=1;j<=n;j++) scanf("%d",&ma[i][j]);
        
        mi=2147483647;
        memset(flag,0,sizeof(flag));
        for (int i=1;i<=n-m+1;i++)
        {
            flag[i]=true;
            dfs(1,i,node[i]);
            flag[i]=false;
        }
        
        int i;
        for (i=1;i<=n;i++) 
        if (outp[i]) 
        {
            printf("%d",i);
            break;
        }
        for (int j=i+1;j<=n;j++)
        if (outp[j]) printf(" %d",j);
        printf("\n");
        scanf("%d%d",&n,&m);
    }
    
    return 0;
}

Related Posts